题目内容
在△ 中,若
中,若 ,则△
,则△ 是( )
是( )
| A.等边三角形 | B.锐角三角形 | C.钝角三角形 | D.直角三角形 |
D
解析试题分析:因为利用向量的加法法则和减法法则得到
因此可知向量的垂直关系,从而得到角C为直角,因此该三角形为直角三角形。
考点:本试题主要考查了向量的数量积的运用,以及运用向量的数量积性质来求解角度和长度问题。
点评:解决该试题的关键是对于向量的加法和减法法则的灵活运用。

练习册系列答案
相关题目
设平面向量 ,
, ,若
,若 ,则
,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
已知 ,则与
,则与 共线的向量为
共线的向量为
A. | B. | C.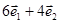 | D. |
已知向量 ,
, ,且
,且 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C. | D. |
正方形ABCD内有一个正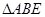 ,设
,设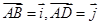 ,则
,则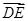 等于
等于
A.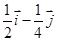 | B.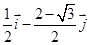 | C.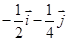 | D.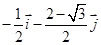 |
已知:如图,  ,
,  与
与 的夹角为
的夹角为 ,
, 与
与 的夹角为
的夹角为 ,若
,若 (
( )则
)则 等于 ( )
等于 ( )
A. | B. | C. | D.2 |
直线 上三点
上三点 ,且点
,且点 分
分 的比为
的比为 ,那么点
,那么点 分
分 的比为( )
的比为( )
A. | B. | C. | D. |
已知A(4,1,3)、B(2,-5,1),C为线段AB上一点, 且 , 则C的坐标为( )
, 则C的坐标为( )
A.( ,- ,- , ,  ) ) | B.( , -3,2) , -3,2) | C.(  , -1, , -1,  ) ) | D.( ,- ,- , ,  ) ) |
 中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )
中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )


