题目内容
解不等式:log8(2-x)+log64(x+1)≥log4x.
思路分析:首先将不等式转化为logaf(x)≥logag(x)的形式.然后利用对数函数的单调性脱掉对数符号,再求解.
解:原不等式可化为
即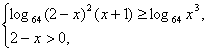
即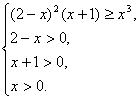
解得{x|0＜x≤
}为所求.
练习册系列答案
相关题目
题目内容
解不等式:log8(2-x)+log64(x+1)≥log4x.
思路分析:首先将不等式转化为logaf(x)≥logag(x)的形式.然后利用对数函数的单调性脱掉对数符号,再求解.
解:原不等式可化为
即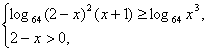
即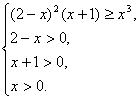
解得{x|0＜x≤}为所求.