题目内容
已知函数 ,求函数的定义域,并讨论它的奇偶性和单调性。
,求函数的定义域,并讨论它的奇偶性和单调性。
 ,求函数的定义域,并讨论它的奇偶性和单调性。
,求函数的定义域,并讨论它的奇偶性和单调性。解:x须满足 ,由
,由 得
得
所以函数的定义域为(-1,0)∪(0,1)
因为函数f(x)的定义域关于原点对称,且对定义域内的任意x,有,

所以f(x)是奇函数
研究f(x)在(0,1)内的单调性,任取x1、x2∈(0,1),且设x1<x2,则


由 ,
,
得 >0,即f(x)在(0,1)内单调递减,由于
>0,即f(x)在(0,1)内单调递减,由于 是奇函数,
是奇函数,
所以 在(-1,0)内单调递减。
在(-1,0)内单调递减。
 ,由
,由 得
得
所以函数的定义域为(-1,0)∪(0,1)
因为函数f(x)的定义域关于原点对称,且对定义域内的任意x,有,

所以f(x)是奇函数
研究f(x)在(0,1)内的单调性,任取x1、x2∈(0,1),且设x1<x2,则


由
 ,
,
得
 >0,即f(x)在(0,1)内单调递减,由于
>0,即f(x)在(0,1)内单调递减,由于 是奇函数,
是奇函数,所以
 在(-1,0)内单调递减。
在(-1,0)内单调递减。
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
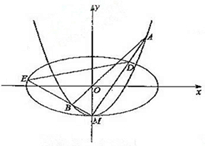 已知椭圆C1:
已知椭圆C1: