题目内容
如图，正方形ABCD中，点P在边CD上，现有质地均匀的粒子散落在正方形ABCD内，则粒子落在△PBA内的概率等于（ ）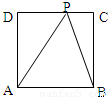
A．
B．
C．
D．
【答案】分析：我们分别求出三角形区域的面积，并求出正方形面积面积用来表示全部基本事件，再代入几何概型公式，即可求解．
解答：解：因为均匀的粒子落在正方形内任何一点是等可能的
所以符合几何概型的条件．
设A=“粒子落在三角形区域”则依题意得
正方形面积为：a×a=a2
三角形的面积为：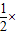
a×a=
a2，
∴P（A）=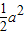
则粒子落在三角形区域的概率是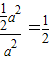
．
故答案为：A
点评：本题考查的知识点是几何概型的意义，简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
解答：解：因为均匀的粒子落在正方形内任何一点是等可能的
所以符合几何概型的条件．
设A=“粒子落在三角形区域”则依题意得
正方形面积为：a×a=a2
三角形的面积为：
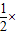a×a=a2，∴P（A）=
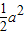
则粒子落在三角形区域的概率是
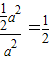．故答案为：A
点评：本题考查的知识点是几何概型的意义，简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
相关题目
如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，AB=
8、如图把正方形ABCD沿对角线BD折成直二面角，对于下面结论：
如图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM=BN=a（0＜a＜
如图，正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD，AE⊥平面CDE．
（2010•温州二模）如图，正方形ABCD与正方形CDEF所成的二面角为60°，则直线EC与直线AD所成的角的余弦值为