题目内容

已知正三棱柱ABC-A1B1C1中，A1B⊥CB1，则A1B与AC1所成的角为
π
2
π
2
．
分析：取AB、A1B1的中点，连接CD、C1E，可证AE、B1D分别是AC1、CB1在平面ABB1A1的射影，由三垂线逆定理得：A1B⊥B1D，再证A1B⊥AE，
然后由三垂线定理得：A1B⊥AC1．
解答：解：取AB、A1B1的中点，连接CD、C1E，
∵三棱柱ABC-A1B1C1是正三棱柱，∴CD⊥平面ABB1A1，C1E⊥平面ABB1A1，
∴AE、B1D分别是AC1、CB1在平面ABB1A1的射影，
∵A1B⊥CB1，由三垂线逆定理得：A1B⊥B1D，
∵AD∥B1E，AD=B1E，∴四边形ADB1E为平行四边形，∴AE∥DB1，
∴A1B⊥AE，
由三垂线定理得：A1B⊥AC1，
∴A1B与AC1所成的角为
π
2
．
故答案为
π
2
．
点评：本题主要考查三垂线定理与逆定理的应用，三垂线定理与逆定理是空间中证明线线垂直的常用方法．
练习册系列答案
相关题目
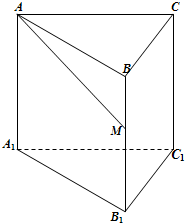精英家教网如图，已知正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞2），动点M在侧棱BB1上移动．设AM与侧面BB1C1C所成的角为θ．
（1）当θ∈[
π
6
，
π
4
]时，求点M到平面ABC的距离的取值范围；
（2）当θ=
π
6
时，求向量
AM
与
BC
夹角的大小．
已知正三棱柱ABC-A1B1C1的每条棱长均为a，M为棱A1C1上的动点．
（1）当M在何处时，BC1∥平面MB1A，并证明之；
（2）在（1）下，求平面MB1A与平面ABC所成的二面角的大小；
（3）求B-AB1M体积的最大值．
已知正三棱柱ABC-A1B1C1，底面边长为8，对角线B1C=10，
（1）若D为AC的中点，求证：AB1∥平面C1BD；
（2）若CD=2AD，BP=λPB1，当λ为何值时，AP∥平面C1BD；
（3）在（1）的条件下，求直线AB1到平面C1BD的距离．
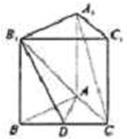精英家教网如图，已知正三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=1．
（1）求证：平面AB1D⊥平面B1BCC1；
（2）求证：A1C∥平面AB1D；
（3）求二面角B-AB1-D的正切值．
（2009•湖北模拟）如图，已知正三棱柱ABC-A1B1C1各棱长都为a，P为棱A1B上的动点．
（Ⅰ）试确定A1P：PB的值，使得PC⊥AB；
（Ⅱ）若A1P：PB=2：3，求二面角P-AC-B的大小；
（Ⅲ）在（Ⅱ）的条件下，求点C1到面PAC的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网