Question

如图,直三棱柱ABC—A₁B₁C₁,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA₁=2,M、N分别是A₁B₁、A₁A的中点,

       (1)求的长；

       (2)求cos〈〉的值；

       (3)求证:A₁B⊥C₁M.

      

Answer 1

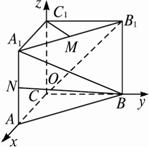
解析:如题图,以C为原点建立空间直角坐标系O—xyz.?

       (1)依题意,得B(0,1,0),N(1,0,1),?

       ∴||=?

       (2)依题意,得A₁(1,0,2),B(0,1,0),C(0,0,0),B₁(0,1,2),?

       ∴={1,-1,2},={0,1,2},=3,||=,||=.?

       ∴cos〈,〉=.　　

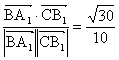       (3)依题意,得C₁(0,0,2),M(,,2),={-1,1,-2},={,,0},?

       ∴·=-++0=0.?

       ∴⊥.   ∴A₁B⊥C₁M.