题目内容
将边长为a的正方形ABCD沿对角线AC折起，使BD=a，则三棱锥D—ABC的体积为( )
A． | B． | C． | D． |
D
解析试题分析：O是AC中点，连接DO，BO，△ADC，△ABC都是等腰直角三角形 ，
，，BD=a，△BDO也是等腰直角三角形 DO⊥AC，DO⊥BO DO⊥平面ABC ，DO就是三棱锥D-ABC的高 ，
S三棱锥D-ABC的体积：
.故选D
考点：棱柱、棱锥、棱台的体积．
练习册系列答案
金钥匙试卷系列答案
相关题目
已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）
A．108 | B．100 | C．92 | D．84 |
；直径为2的球的体积为
．则
()
一个几何体的三视图如图所示，则该几何体的体积为
| A．2 | B．1 | C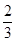． | D． |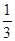
一几何体的三视图如图所示,则该几何体的体积为（ ）
| A．200+9π | B．200+18π | C．140+9π | D．140+18π |
的三边长分别为a、b、c，
；类比这个结论可知：四面体P－ABC的四个面的面积分别为S1、S2、S3、S4，内切球的半径为r，四面体
.
.
.
.
设四面体
各棱长均相等, 
为
的中点, 
为
上异于中点和端点的任一点,则
在四面体的面
上的的射影可能是
| A．① | B．② | C．③ | D．④ |
某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）
A． | B． | C． | D． |