题目内容
已知数列{an}的前n项和为Sn,满足关系式(2+t)Sn+1-tSn=2t+4(t≠-2,t≠0,n=1,2,3,…).
(Ⅰ)当a1为何值时,数列{an}是等比数列;
(Ⅱ)在(Ⅰ)的条件下,设数列{an}的公比为f(t),作数列{bn}使b1=1,bn=f(bn-1)(n=2,3,4,…),求bn;
(Ⅲ)在(Ⅱ)条件下,如果对一切n∈N+,不等式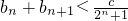 恒成立,求实数c的取值范围.
恒成立,求实数c的取值范围.
解:(Ⅰ)(2+t)Sn+1-tSn=2t+4①n≥2时,(2+t)Sn-tSn-1=2t+4②
两式相减:(2+t)(Sn+1-Sn)-t(Sn-Sn-1)=0,(2+t)an+1-tan=0, .即n≥2时,
.即n≥2时, 为常数
为常数 .(2分)
.(2分)
当n=1时,(2+t)S2-tS1=2t+4,(2+t)(a2+a1)-ta1=2t+4,解得 .
.
要使{an}是等比数列,必须 .∴
.∴ ,解得a1=2.(5分)
,解得a1=2.(5分)
(Ⅱ)由(1)得, ,因此有
,因此有 ,
,
即 ,整理得
,整理得 .
.
则数列 是首项为
是首项为 =2,公比为2的等比数列,
=2,公比为2的等比数列, ,
,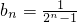 .(10分)
.(10分)
(Ⅲ)把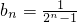 ,
, 代入得:
代入得: ,
,
即 ,
,
要使原不等式恒成立,c必须比上式右边的最大值大.∵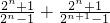 =
= ,
,
∴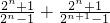 的值随n的增大而减小.则当n=1时,
的值随n的增大而减小.则当n=1时,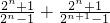 取得最大值4.
取得最大值4.
因此,实数c的取值范围是c>4.(14分)
分析:(Ⅰ)由(2+t)Sn+1-tSn=2t+4,知(2+t)(Sn+1-Sn)-t(Sn-Sn-1)=0,所以 为常数
为常数 .当n=1时,(2+t)S2-tS1=2t+4,(2+t)(a2+a1)-ta1=2t+4,解得
.当n=1时,(2+t)S2-tS1=2t+4,(2+t)(a2+a1)-ta1=2t+4,解得 .要使{an}是等比数列,必须
.要使{an}是等比数列,必须 ,由此能求出a1.
,由此能求出a1.
(Ⅱ)由 ,知
,知 ,即
,即 .由此能求出bn.
.由此能求出bn.
(Ⅲ)把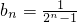 ,
, 代入得:
代入得: ,即
,即 ,要使原不等式恒成立,c必须比上式右边的最大值大由此入手,能求出实数c的取值范围.
,要使原不等式恒成立,c必须比上式右边的最大值大由此入手,能求出实数c的取值范围.
点评:本题考查数列的性质和应用,解题时要认真审题,注意公式的合理运用.
两式相减:(2+t)(Sn+1-Sn)-t(Sn-Sn-1)=0,(2+t)an+1-tan=0,
 .即n≥2时,
.即n≥2时, 为常数
为常数 .(2分)
.(2分)当n=1时,(2+t)S2-tS1=2t+4,(2+t)(a2+a1)-ta1=2t+4,解得
 .
.要使{an}是等比数列,必须
 .∴
.∴ ,解得a1=2.(5分)
,解得a1=2.(5分)(Ⅱ)由(1)得,
 ,因此有
,因此有 ,
,即
 ,整理得
,整理得 .
.则数列
 是首项为
是首项为 =2,公比为2的等比数列,
=2,公比为2的等比数列, ,
,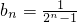 .(10分)
.(10分)(Ⅲ)把
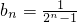 ,
, 代入得:
代入得: ,
,即
 ,
,要使原不等式恒成立,c必须比上式右边的最大值大.∵
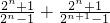 =
= ,
,∴
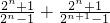 的值随n的增大而减小.则当n=1时,
的值随n的增大而减小.则当n=1时,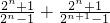 取得最大值4.
取得最大值4.因此,实数c的取值范围是c>4.(14分)
分析:(Ⅰ)由(2+t)Sn+1-tSn=2t+4,知(2+t)(Sn+1-Sn)-t(Sn-Sn-1)=0,所以
 为常数
为常数 .当n=1时,(2+t)S2-tS1=2t+4,(2+t)(a2+a1)-ta1=2t+4,解得
.当n=1时,(2+t)S2-tS1=2t+4,(2+t)(a2+a1)-ta1=2t+4,解得 .要使{an}是等比数列,必须
.要使{an}是等比数列,必须 ,由此能求出a1.
,由此能求出a1.(Ⅱ)由
 ,知
,知 ,即
,即 .由此能求出bn.
.由此能求出bn.(Ⅲ)把
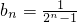 ,
, 代入得:
代入得: ,即
,即 ,要使原不等式恒成立,c必须比上式右边的最大值大由此入手,能求出实数c的取值范围.
,要使原不等式恒成立,c必须比上式右边的最大值大由此入手,能求出实数c的取值范围.点评:本题考查数列的性质和应用,解题时要认真审题,注意公式的合理运用.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |