题目内容
过函数y=sin2x+1图象上的点M(
,
)作该函数图象的切线,则这条切线方程是 ( )
| π |
| 4 |
| 3 |
| 2 |
分析:求导函数,确定切线的斜率,利用点斜式,即可得到切线方程.
解答:解:求导函数可得y′=2sinxcosx=sin2x
∴x=
时,y′=1
∴所求切线方程为y-
=x-
,即y=x+
-
故选D.
∴x=
| π |
| 4 |
∴所求切线方程为y-
| 3 |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 4 |
故选D.
点评:本题考查导数的几何意义,考查切线方程,考查学生的计算能力,属于基础题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
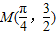 作该函数图象的切线,则这条切线方程是 ( )
作该函数图象的切线,则这条切线方程是 ( )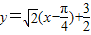
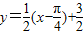
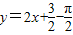
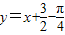
 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x- )的图象.
)的图象.