Question

求证：当且仅当n是3的倍数时，等比数列1，2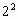，，…的前n项和能被7整除．

Answer 1

答案：
解析：

证明 =1＋2＋＋…＋=－1 当n=1，2时，显然不能被7整除． 当n≥3时，设n=3k＋r，k∈，r∈{0，1，2}，则 易知能被7整除，且 r=0时，－1=0； r=1时，－1=1； r=2时，－1=3． ∴当且仅当r＝0即n是3的整数倍时，能被7整除． 注意，本例也可用数学归纳法证明．利用二项式定理证明有关多项式的整除问题，关键在于将被除式构造成恰当的二项式形式，使其展开后的每一项均含有除式的因式．