题目内容
已知a>0,b>0,且a+b="1." 求证: (a+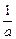 )(b+
)(b+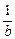 )≥
)≥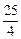 .
.
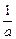 )(b+
)(b+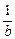 )≥
)≥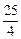 .
.证明略
证法一:(分析综合法)
欲证原式,即证4(ab)2+4(a2+b2)-25ab+4≥0,
即证4(ab)2-33(ab)+8≥0,即证ab≤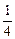 或ab≥8.
或ab≥8.
∵a>0,b>0,a+b=1,∴ab≥8不可能成立
∵1=a+b≥2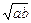 ,∴ab≤
,∴ab≤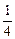 ,从而得证.
,从而得证.
证法二:(均值代换法)
设a= +t1,b=
+t1,b= +t2.
+t2.
∵a+b=1,a>0,b>0,∴t1+t2=0,|t1|< ,|t2|<
,|t2|<
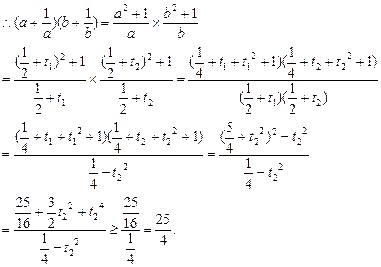
显然当且仅当t=0,即a=b= 时,等号成立.
时,等号成立.
证法三:(比较法)
∵a+b=1,a>0,b>0,∴a+b≥2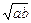 ,∴ab≤
,∴ab≤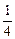
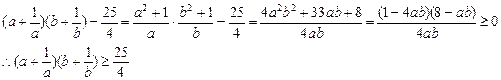
证法四:(综合法)
∵a+b=1,a>0,b>0,∴a+b≥2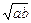 ,∴ab≤
,∴ab≤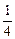 .
.
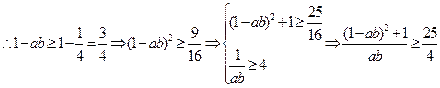
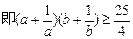
证法五:(三角代换法)
∵a>0,b>0,a+b=1,故令a=sin2α,b=cos2α,α∈(0,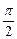 )
)
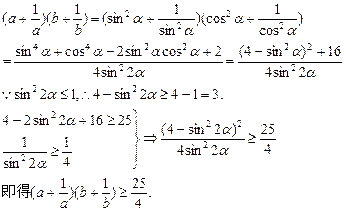
欲证原式,即证4(ab)2+4(a2+b2)-25ab+4≥0,
即证4(ab)2-33(ab)+8≥0,即证ab≤
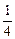 或ab≥8.
或ab≥8. ∵a>0,b>0,a+b=1,∴ab≥8不可能成立
∵1=a+b≥2
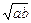 ,∴ab≤
,∴ab≤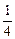 ,从而得证.
,从而得证.证法二:(均值代换法)
设a=
 +t1,b=
+t1,b= +t2.
+t2.∵a+b=1,a>0,b>0,∴t1+t2=0,|t1|<
 ,|t2|<
,|t2|<
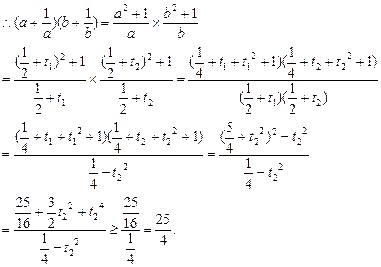
显然当且仅当t=0,即a=b=
 时,等号成立.
时,等号成立.证法三:(比较法)
∵a+b=1,a>0,b>0,∴a+b≥2
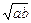 ,∴ab≤
,∴ab≤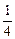
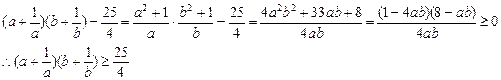
证法四:(综合法)
∵a+b=1,a>0,b>0,∴a+b≥2
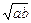 ,∴ab≤
,∴ab≤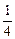 .
. 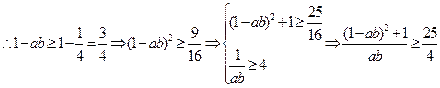
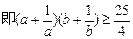
证法五:(三角代换法)
∵a>0,b>0,a+b=1,故令a=sin2α,b=cos2α,α∈(0,
 )
)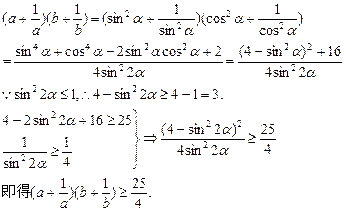

练习册系列答案
相关题目
 。
。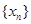 对一切
对一切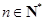 均满足
均满足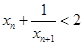 .证明:
.证明: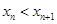 ;
;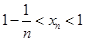 .
.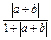 ≤
≤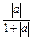 +
+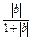 .
.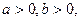 求证
求证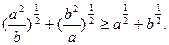
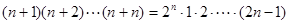 ”(
”( )时,从 “
)时,从 “ ”时,左边应增添的式子是( )
”时,左边应增添的式子是( )



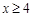 时,求证:
时,求证: