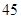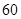题目内容
某次数学测试6位同学成绩的茎叶图如下,将这6位同学成绩作为总体,从总体中任取两位同学成绩作为一个样本,则样本平均数大于总体平均数的概率是( )
A. | B. | C. | D. |
A
解析试题分析:从6个样本中任取2个,总的方法数为 =15,这组数据为56,65,66,68,74,80,平均数为
=15,这组数据为56,65,66,68,74,80,平均数为 ,从总体中任取两位同学成绩作为一个样本,样本平均数大于总体平均数的有(80,74),(80,68),(80,66)(80,65),(74,68),(74,66),(74,65),所以,样本平均数大于总体平均数的概率是
,从总体中任取两位同学成绩作为一个样本,样本平均数大于总体平均数的有(80,74),(80,68),(80,66)(80,65),(74,68),(74,66),(74,65),所以,样本平均数大于总体平均数的概率是 ,故选A。
,故选A。
考点:茎叶图,平均数,古典概型概率的计算。
点评:简单题,古典概型的概率计算,关键是弄清两个“事件数”,常常采用“树图法”、“坐标法”。

从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示).设甲乙两组数据的平均数分别为 甲,
甲, 乙,中位数分别为m甲,m乙,则( ).
乙,中位数分别为m甲,m乙,则( ).
A. 甲< 甲< 乙,m甲>m乙 乙,m甲>m乙 | B. 甲< 甲< 乙,m甲<m乙 乙,m甲<m乙 |
C. 甲> 甲> 乙,m甲>m乙 乙,m甲>m乙 | D. 甲> 甲> 乙,m甲<m乙 乙,m甲<m乙 |
有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法所确定的编号有可能是( ).
| A.3, 8,13,18 | B. 2,6,10,14 | C. 2,4,6,8 | D. 5,8,11,14 |
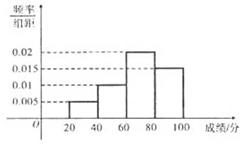
为了了解某地区高三学生的身体素质情况,抽查了该地区 名年龄为17.5岁-18岁的男生体重(
名年龄为17.5岁-18岁的男生体重( ) ,得到频率分布直方图如下
) ,得到频率分布直方图如下
根据上图可得这 名学生中体重在[56.5,64.5]的学生人数是( )
名学生中体重在[56.5,64.5]的学生人数是( )
A. | B.30 | C. | D.50 |
右表是某厂1~4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是 ,则a等于( ).
,则a等于( ).
| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 5.5 | 5 | 4 | 3.5 |
某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图,则上班、下班时间行驶速度的中位数分别是( )
| A.28 27.5 | B.28 28.5 |
| C.29 27.5 | D.29 28.5 |
工人月工资(元)依劳动产值(千元)变化的回归直线方程为 =60+90x,下列判断正确的是( )
=60+90x,下列判断正确的是( )
| A.劳动产值为1 000元时,工资为50元 |
| B.劳动产值提高1 000元时,工资提高150元 |
| C.劳动产值提高1 000元时,工资提高90元 |
| D.劳动产值为1 000元时,工资为90元 |

 若低于60分的人数是15人,则该班的学生人数是( )
若低于60分的人数是15人,则该班的学生人数是( )