题目内容
已知函数![]() 定义在区间[一1,1]上,且
定义在区间[一1,1]上,且![]() ,又P(
,又P(![]() )、Q(
)、Q(![]() )是其图像上任意两点(
)是其图像上任意两点(![]() ).
).
(1)求证:![]() 的图像关于点(0,b)成中心对称图形;
的图像关于点(0,b)成中心对称图形;
(2)设直线PQ的斜率为![]() ,求证:
,求证:![]() <2;
<2;
(3)若0≤![]() ≤1,求证:
≤1,求证:![]() <1.
<1.
解:(1)∵![]() ,∴
,∴![]() ,得
,得![]() .
.
∴![]() ,
,
其图像可由![]() 的图像向上(或下)平移
的图像向上(或下)平移![]() (或
(或![]() )个单位而得到.
)个单位而得到.
又![]() 是奇函数,其图像关于原点成中心对称图形,
是奇函数,其图像关于原点成中心对称图形,
∴![]() 的图像关于点(0,
的图像关于点(0,![]() )成中心对称图形.
)成中心对称图形.
(2)∵点P(![]() )、Q(
)、Q(![]() )在
)在![]() 的图像上,
的图像上,
∴![]()
=![]() .
.
又![]() ∈[一1,1],
∈[一1,1],![]() ,
,
∴![]()
![]() <2,
<2,
从而-1<![]() <2
<2
∴![]() =|
=|![]() |<2.
|<2.
(3)∵0≤![]() ≤1,且
≤1,且![]() ①
①
又![]()
![]()
≤![]()
≤![]()
=![]()
=![]() ②
②
①+②得![]() ,故
,故![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 定义在区间
定义在区间 上,
上, ,且当
,且当 时,
时, .又数列
.又数列 满足
满足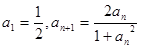 .
. 的表达式;
的表达式; 为数列
为数列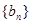 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.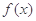 定义在区间
定义在区间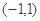 上,
上,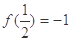 ,且当
,且当 时,恒有
时,恒有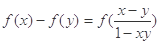 .又数列
.又数列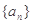 满足
满足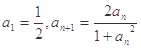 .
.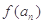 的表达式;
的表达式;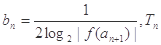 为数列
为数列 的前
的前 项和,若
项和,若 对
对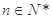 恒成立,求
恒成立,求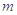 的最小值.
的最小值. 定义在区间
定义在区间 ,对任意
,对任意 ,恒有
,恒有 成立,又数列
成立,又数列 满足
满足 (I)在(-1,1)内求一个实数t,使得
(I)在(-1,1)内求一个实数t,使得 (II)求证:数列
(II)求证:数列 是等比数列,并求
是等比数列,并求 的表达式;(III)设
的表达式;(III)设 ,是否存在
,是否存在 ,使得对任意
,使得对任意 ,
, 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。