Question

已知曲线y =  +  ．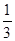

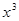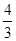（1）求曲线在点A（2 ，4）处的切线方程 ；

（2）求曲线的切线与坐标轴围成的三角形的面积 ．

 

Answer 1

【答案】

（1）y－4 = 4(x－2)

（2）S = ×1×4 = 2 ．

【解析】

解 ：（1）由y =  + 得

 =  ，

∴ k = = 4 ，

∴ 所求切线方程为y－4 = 4(x－2) ,

即 4 x －y－4 = 0 ；

（2）由（1）知曲线的切线方程为4 x －y－4 = 0 ，那么切线与两坐标轴的交点为（1 ，0），（0 ，－4），

∴所求三角形的面积为

S = ×1×4 = 2 ．