Question

已知函数f(x)=

x+ 1 x (x≥ 1 2 ) x+2(x＜ 1 2 )

，f(x)-a=0的三个实数根分别为x₁，x₂，x₃，则x₁x₂x₃的范围是（　　）

• A、（0，+∞）
• B、（0，

  3

  2

  ）
• C、（0，

  1

  2

  ）
• D、(

  1

  2

  ，

  3

  2

  )

Answer 1

分析：作出函数f（x）的图象，根据方程f（x）-a=0有三个不同的实根，求出a的取值范围，然后利用分段函数分别求出x₁，x₂，x₃，之间的关系，即可得到结论．

解答：解：作出函数f（x）的图象如图：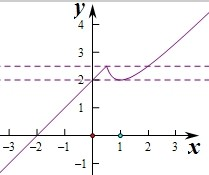
当x=1，f（x）=2，当x=

1

2

，f（x）=

5

2

，
∴要使f（x）-a=0有三个实数根，则2＜a＜

5

2

，
不妨设x₁＜x₂＜x₃．
由f（x）=x+2=a，
解得x=a-2，
即x₁+2=a
∴x₁=a-2
由f（x）=x+

1

x

=a，
即x²-ax+1=0，
由韦达定理可知：x₂x₃=1，
∴x₁x₂x₃=a-2
∵a∈（2，

5

2

）
∴a-2∈（0，

1

2

）
∴x₁x₂x₃∈（0，

1

2

）
故选：C．

点评：本题主要考查方程根的个数的应用，利用数形结合确定a的取值范围是解决本题的关键，综合性较强，难度较大．