题目内容
已知数列{an}的各项都是正数,且满足:a0=1,an+1=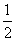 an(4-an),n∈N,
an(4-an),n∈N,
(1)证明an<an+1<2,n∈N;
(2)求数列{an}的通项公式an。
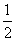 an(4-an),n∈N,
an(4-an),n∈N, (1)证明an<an+1<2,n∈N;
(2)求数列{an}的通项公式an。
解:(1)用数学归纳法证明:
1°当n=1时,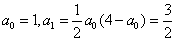 ,
,
∴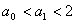 ,命题正确;
,命题正确;
2°假设n=k时有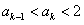 ,
,
则n=k+1时,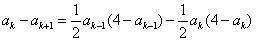
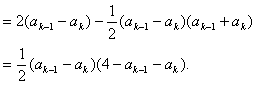
而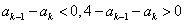 ,
,
∴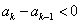 ,
,
又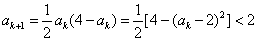 ,
,
∴n=k+1时命题正确;
由1°、2°知,对一切n∈N时有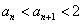 。
。
(2)下面来求数列的通项: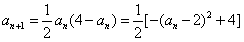 ,
,
所以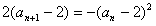 ,
,
令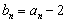 ,
,
则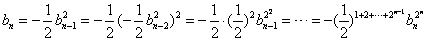 ,
,
又bn=-1,
所以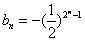 ,即
,即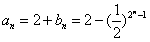 。
。
1°当n=1时,
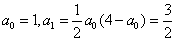 ,
, ∴
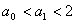 ,命题正确;
,命题正确;2°假设n=k时有
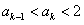 ,
,则n=k+1时,
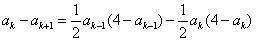
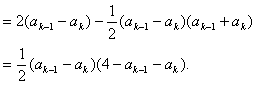
而
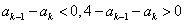 ,
,∴
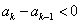 ,
,又
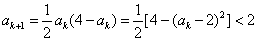 ,
, ∴n=k+1时命题正确;
由1°、2°知,对一切n∈N时有
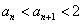 。
。(2)下面来求数列的通项:
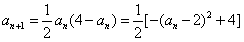 ,
,所以
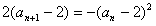 ,
,令
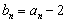 ,
,则
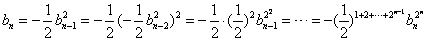 ,
,又bn=-1,
所以
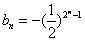 ,即
,即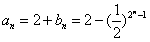 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)