题目内容
已知定义域为R的函数 是奇函数。
是奇函数。
(1)求f(x);
(2)是否存在最大的常数k,对于任意实数都有f(x)>k,求出k;若不存在,说明理由;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围。
 是奇函数。
是奇函数。(1)求f(x);
(2)是否存在最大的常数k,对于任意实数都有f(x)>k,求出k;若不存在,说明理由;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围。
解:(1)因为f(x)是R上的奇函数,所以f(0)=0,即 ,解得:b=1,
,解得:b=1,
从而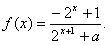 ;
;
又由f(1)= -f(-1)知 ,解得:a=2,
,解得:a=2,
∴ 。
。
(2)由(1)知
由上式易知f(x)在R上为减函数,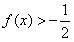 ,所以k=
,所以k=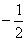 。
。
(3)由(1)知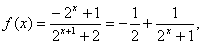
由上式易知f(x)在R上为减函数,
又因f(x)是奇函数,
从而不等式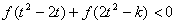 等价于
等价于 ,
,
因f(x)是R上的减函数,由上式推得,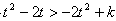 ,
,
即对一切t∈R有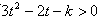 ,
,
从而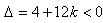 ,解得:
,解得: 。
。
 ,解得:b=1,
,解得:b=1,从而
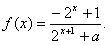 ;
;又由f(1)= -f(-1)知
 ,解得:a=2,
,解得:a=2,∴
 。
。(2)由(1)知

由上式易知f(x)在R上为减函数,
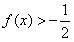 ,所以k=
,所以k=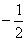 。
。(3)由(1)知
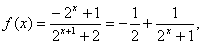
由上式易知f(x)在R上为减函数,
又因f(x)是奇函数,
从而不等式
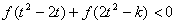 等价于
等价于 ,
,因f(x)是R上的减函数,由上式推得,
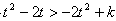 ,
,即对一切t∈R有
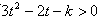 ,
,从而
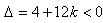 ,解得:
,解得: 。
。
练习册系列答案
相关题目