题目内容
(本小题满分12分)
右图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人

(I)求该专业毕业总人数N和90~95分数段内的人数 ;
;
(II)现欲将90~95分数段内的 名人分配到几所学校,从中安排2人到甲学校去,若
名人分配到几所学校,从中安排2人到甲学校去,若 人中仅有两名男生,求安排结果至少有一名男生的概率.
人中仅有两名男生,求安排结果至少有一名男生的概率.
(I)6;(II) .
.
【解析】
试题分析:(1)解决频率分布直方图的问题,关键在于找出图中数据之间的关系,这些数据中,比较明显的有组距、 ,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)频率分布直方图中,注意小矩形的高是
,间接的有频率,小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形的面积等于频率,小长方形的面积之和等于1,因此频率之和为1;(2)频率分布直方图中,注意小矩形的高是 ,而不是频率.(3)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举.
,而不是频率.(3)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举.
试题解析:(Ⅰ) 分数段频率为
分数段频率为 ,此分数段的学员总数为
,此分数段的学员总数为 人所以毕业生的总人数
人所以毕业生的总人数 为
为 3分
3分
 分数段内的人数频率为
分数段内的人数频率为 所以
所以 分数段内的人数
分数段内的人数 6分
6分
(Ⅱ)  分数段内的
分数段内的 人中有两名男生,
人中有两名男生, 名女生
名女生
设男生为 ;女生为
;女生为 ,设安排结果中至少有一名男生为事件
,设安排结果中至少有一名男生为事件
从中取两名毕业生的所有情况(基本事件空间)为
9分
共 种组合方式,每种组合发生的可能性是相同的
种组合方式,每种组合发生的可能性是相同的
其中, 至少有一名男生的种数为 共
共 种
种
所以, 12分
12分
考点:频率分布直方图及古典概型.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目

 (B)
(B)

 的各实根为
的各实根为 .若点
.若点 均在直线
均在直线 的同侧,则实数
的同侧,则实数 的取值范围是( )
的取值范围是( ) B.
B. 
 D.
D. 
 ,则输出的
,则输出的

 B.
B.  C.
C.  D.
D. 
 ,则
,则
 B.
B.  C.
C.  D.
D. 
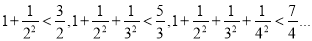 则可归纳出关于正整数
则可归纳出关于正整数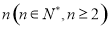 的式子为__________________.
的式子为__________________. 是方程
是方程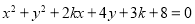 表示圆的充要条件;
表示圆的充要条件;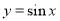 的图象向右平移
的图象向右平移 单位,再保持纵坐标不变,横坐标变为原来的
单位,再保持纵坐标不变,横坐标变为原来的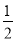 ,得到函数
,得到函数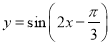 的图象;
的图象;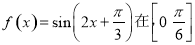 上为增函数;
上为增函数;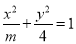 的焦距为2,则实数m的值等于5.
的焦距为2,则实数m的值等于5.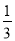 ,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为 B.
B. 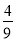 C.
C. 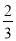 D.
D. 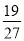
 中,
中, 分别为
分别为 的中点,记三棱锥
的中点,记三棱锥 的体积为
的体积为 ,
, 的体积为
的体积为 ,则
,则