题目内容
己知向量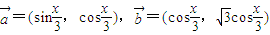 ,函数
,函数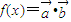 .
.(1)求f(x)的最小正周期和单调减区间;
(2)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求此时函数f(x)的值域.
【答案】分析:(1)根据函数 进而利用两角和公式化简整理求得f(x)=
进而利用两角和公式化简整理求得f(x)= 进而根据正弦函数的周期性求得最小正周期.进而根据正弦函数的单调性求得其单调减区间.
进而根据正弦函数的周期性求得最小正周期.进而根据正弦函数的单调性求得其单调减区间.
(2)把b2=ac代入余弦定理求得cosx的值,进而根据x的范围求得 的范围,进而确定函数的最大和最小值,求得函数的值域.
的范围,进而确定函数的最大和最小值,求得函数的值域.
解答:解:(1)
=
=

令
∴
单调原函数的减区间为
(2)由已知b2=ac


∴
∵ ,
,
∴
 ≤1,
≤1,
∴ .
.
即f(x)的值域为 .
.
点评:本题主要考查了正弦函数的单调性,周期性和值域问题.考查了学生综合分析问题和解决问题的能力.
 进而利用两角和公式化简整理求得f(x)=
进而利用两角和公式化简整理求得f(x)= 进而根据正弦函数的周期性求得最小正周期.进而根据正弦函数的单调性求得其单调减区间.
进而根据正弦函数的周期性求得最小正周期.进而根据正弦函数的单调性求得其单调减区间.(2)把b2=ac代入余弦定理求得cosx的值,进而根据x的范围求得
 的范围,进而确定函数的最大和最小值,求得函数的值域.
的范围,进而确定函数的最大和最小值,求得函数的值域.解答:解:(1)

=

=


令

∴

单调原函数的减区间为

(2)由已知b2=ac


∴

∵
 ,
,∴

 ≤1,
≤1,∴
 .
.即f(x)的值域为
 .
.点评:本题主要考查了正弦函数的单调性,周期性和值域问题.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
 ,函数
,函数 .
.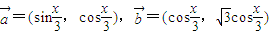 ,函数
,函数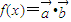 .
.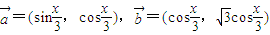 ,函数
,函数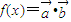 .
.