题目内容
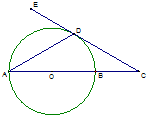（2012•东城区一模）如图，AB是⊙O的直径，直线DE切⊙O于点D，且与AB延长线交于点C，若CD=| 3 |
60°
60°
．分析：由切割线定理可得，CD2=CB•CA可求AC，进而可求CO，连接OD，则可得Rt△ODC中，∠DOC=60°=∠OBD，，再由弦切角定理可得，∠ADE=∠ABD，可求
解答：解：∵CD=
，CB=1
由切割线定理可得，CD2=CB•CA
∴CA=3，BA=2
∴CO=2
连接OD，则可得OD⊥CD
Rt△ODC中，OD=1，CO=2，CD=
∴∠DOC=60°
∵△BOD中，OB=OD
∴∠OBD=60°
由弦切角定理可得，∠ADE=∠ABD=60°
故答案为：60°
| 3 |
由切割线定理可得，CD2=CB•CA
∴CA=3，BA=2
∴CO=2
连接OD，则可得OD⊥CD
Rt△ODC中，OD=1，CO=2，CD=
| 3 |
∴∠DOC=60°
∵△BOD中，OB=OD
∴∠OBD=60°
由弦切角定理可得，∠ADE=∠ABD=60°
故答案为：60°
点评：本题主要考查了圆的切割线定理、弦切角定理的综合应用，解题的关键是熟练应用基本知识
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
（2012•东城区一模）已知函数f（x）=（x-a）（x-b）（其中a＞b），若f（x）的图象如图所示，则函数g（x）=ax+b的图象大致为．（ ）
（2012•东城区一模）在如图所示的茎叶图中，乙组数据的中位数是
（2012•东城区一模）如图1，在边长为3的正三角形ABC中，E，F，P分别为AB，AC，BC上的点，且满足AE=FC=CP=1．将△AEF沿EF折起到△A1EF的位置，使平面A1EF⊥平面EFB，连接A1B，A1P．（如图2）