题目内容
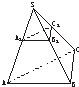13、如图，设不全等的△ABC与△A1B1C1不在同一平面内，且AB∥A1B1，BC∥B1C1，CA∥C1A1．求证：AA1、BB1、CC1三线共点．
分析：要证明三线共点，可以先设定其中两条的交点，然后再证明这个交点在第三条线上，观察图形可以发现CC1即为面BCC1B1与面ACC1A1的交线，而直线AA1、BB1又分别在面ACC1A1、面BCC1B1内，所以直线AA1、BB1的交点就应该在交线CC1上，即三线共点．
解答：证明：不妨设AB≠A1B1，AA1∩BB1=S，
∵BC∥B1C1，
∴BB1?面BCC1B1，S∈面BCC1B1．
同理，S∈面ACC1A1．
∴S∈CC1，
即AA1、BB1、CC1三线共点于S．
∵BC∥B1C1，
∴BB1?面BCC1B1，S∈面BCC1B1．
同理，S∈面ACC1A1．
∴S∈CC1，
即AA1、BB1、CC1三线共点于S．
点评：此题主要考查的知识点是公理2的应用，是常见题型，经典题．
练习册系列答案
相关题目
一块边长为10的正方形纸片，按如图所示将阴影部分裁下，然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD（底面是正方形，顶点在底面的射影是底面中心的四棱锥）．
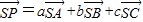（a+b+c=1），在第（1）问的条件下，求
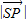的最小值，并求取得最小值时a，b，c的值；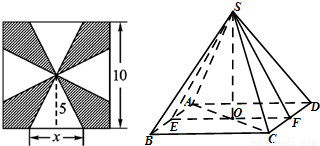
（a+b+c=1），在第（1）问的条件下，求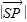
的最小值，并求取得最小值时a，b，c的值；