题目内容
已知:0<a<b<c<d 且a+d=b+c,求证: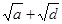 <
< 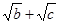
见解析
解析试题分析:
直接证明显然不容易入手,所以采用分析法证明,从要证明的不等式出发,寻找使这个不等式成立的某一"充分的"条件,为此逐步往前追溯(执果索因),一直追溯到已知条件或一些真命题为止.
根据题意可知, 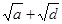 和
和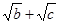 都是正数,所以为了证明结论,给不等式两边同时平方,而后根据题意
都是正数,所以为了证明结论,给不等式两边同时平方,而后根据题意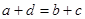 ,只需证明
,只需证明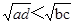 ,将其平方,可得
,将其平方,可得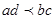 .由于不等式中含有四个未知数,所以可利用其中三个将另一个表示出来,不妨消掉
.由于不等式中含有四个未知数,所以可利用其中三个将另一个表示出来,不妨消掉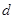 ,即
,即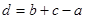 ,带入
,带入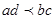 ,化简可得
,化简可得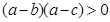 ,根据题意,
,根据题意,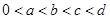 ,该不等式显然成立.所以该不等式得证.
,该不等式显然成立.所以该不等式得证.
试题解析:因为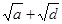 和
和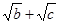 都是正数,
都是正数,
所以为了证明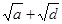 <
<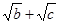
只需证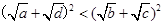
只需证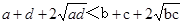
而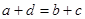
即证 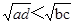
即证 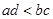
又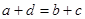 所以
所以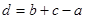
即证: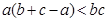
即证: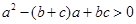
即证: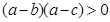
而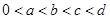
所以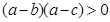 显然成立
显然成立
所以原不等式成立。
考点:分析法证明不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
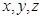 满足
满足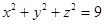 ,则
,则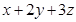 的最大值是 .
的最大值是 .  ,则a,b,c的大小关系是 .
,则a,b,c的大小关系是 .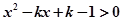 对
对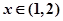 恒成立,则实数
恒成立,则实数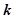 的取值范围是______.
的取值范围是______. +abc≥2
+abc≥2 .
.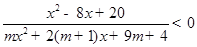 的解集为
的解集为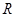 ,求实数
,求实数 的取值范围。
的取值范围。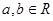 ,
,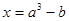 ,
,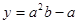 ,试比较
,试比较 与
与 的大小.
的大小.