题目内容
3.a为实数,函数f(x)=|x2-ax|在区间[0,1]上的最大值记为g(a).当a=2$\sqrt{2}$-2时,g(a)的值最小.分析 通过分a≤0、0<a≤2$\sqrt{2}$-2、a>2$\sqrt{2}$-2三种情况去函数f(x)表达式中绝对值符号,利用函数的单调性即得结论.
解答 解:对函数f(x)=|x2-ax|=|(x-$\frac{a}{2}$)2-$\frac{{a}^{2}}{4}$|分下面几种情况讨论:
①当a≤0时,f(x)=x2-ax在区间[0,1]上单调递增,
∴f(x)max=g(1)=1-a;
②当0<a≤2$\sqrt{2}$-2时,$f(\frac{a}{2})$=$|(\frac{a}{2})^{2}-a×\frac{a}{2}|$=$\frac{{a}^{2}}{4}$,f(1)=1-a,
∵$\frac{{a}^{2}}{4}$-(1-a)=$\frac{(a+2)^{2}}{4}$-2<0,
∴f(x)max=g(1)=1-a;
③当2$\sqrt{2}$-2<a≤1时,f(x)max=g(a)=$\frac{{a}^{2}}{4}$;
综上所述,g(a)=$\left\{\begin{array}{l}{1-a,0<a<2\sqrt{2}-2}\\{\frac{{a}^{2}}{4},2\sqrt{2}-2<a≤1}\end{array}\right.$,
∴g(a)在(-∞,$2\sqrt{2}-2$]上单调递减,在[$2\sqrt{2}-2$,+∞)上单调递增,
∴g(a)min=g($2\sqrt{2}-2$);
④当1<a<2时,g(a)=f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$;
⑤当a≥2时,g(a)=f(1)=a-1;
综上,当a=$2\sqrt{2}-2$时,g(a)min=3-2$\sqrt{2}$,
故答案为:$2\sqrt{2}-2$.
点评 本题考查求函数的最值,考查分类讨论的思想,注意解题方法的积累,属于难题.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案| A. | ($\frac{7}{4}$,+∞) | B. | (-∞,$\frac{7}{4}$) | C. | (0,$\frac{7}{4}$) | D. | ($\frac{7}{4}$,2) |
| A. | A=B | B. | A∩B=∅ | C. | A$\stackrel{?}{≠}$B | D. | B$\stackrel{?}{≠}$A |
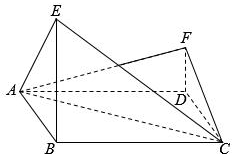 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.