题目内容
上海迪斯尼乐园的具体建设在紧锣密鼓的推进之中,要形成一定规模的主题乐园至少还需要四到五年的时间,其中有三名工人准备参与建设“动物王国”、“魔幻影城”和“梦幻世界”三个主题公园,规划中3个主题公园所含工程项目的个数分别占总工程个数的| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
(1)求他们选择的项目互不相同的概率.
(2)记ξ为3人中选择的项目属于“魔幻影城”或“梦幻世界”的人数,求ξ的分布列及数学期望.
分析:第i名工人选择“动物王国”、“魔幻影城”和“梦幻世界”分别为事件Ai,Bi,Ci(i=1,2,3).
知A1,A2,A3相互独立,B1,B2,B3相互独立,C1,C2,C3相互独立,
且P(Ai)=
,P(Bi)=
,P(Ci)=
(1)他们选择的项目互不相同的概率P=6P(A1B2C3),代入可求
(2)第i名工人选择的项目属于“魔幻影城”或“梦幻世界”为事件Di,
P(Di)=P(Bi+Ci)=P(Bi)+P(Ci),代入分别求出概率后,列出分布列,求出期望即可
知A1,A2,A3相互独立,B1,B2,B3相互独立,C1,C2,C3相互独立,
且P(Ai)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)他们选择的项目互不相同的概率P=6P(A1B2C3),代入可求
(2)第i名工人选择的项目属于“魔幻影城”或“梦幻世界”为事件Di,
P(Di)=P(Bi+Ci)=P(Bi)+P(Ci),代入分别求出概率后,列出分布列,求出期望即可
解答:解:记第i名工人选择“动物王国”、“魔幻影城”和“梦幻世界”分别为事件Ai,Bi,Ci(i=1,2,3).
知A1,A2,A3相互独立,B1,B2,B3相互独立,C1,C2,C3相互独立,
且P(Ai)=
,P(Bi)=
,P(Ci)=
(1)他们选择的项目互不相同的概率P=6P(A1B2C3)=6×
×
×
=
(2)第i名工人选择的项目属于“魔幻影城”或“梦幻世界”为事件Di(i=1,2,3).
知D1,D2,D3相互独立,且P(Di)=P(Bi+Ci)=P(Bi)+P(Ci)=
+
=
,所以,ξ-B(3,
)
即P(ξ=k)=C3k(
)k(1-
)3-k(k=0,1,2,3)故ξ的分布列是:

Eξ=
知A1,A2,A3相互独立,B1,B2,B3相互独立,C1,C2,C3相互独立,
且P(Ai)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)他们选择的项目互不相同的概率P=6P(A1B2C3)=6×
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
(2)第i名工人选择的项目属于“魔幻影城”或“梦幻世界”为事件Di(i=1,2,3).
知D1,D2,D3相互独立,且P(Di)=P(Bi+Ci)=P(Bi)+P(Ci)=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
即P(ξ=k)=C3k(
| 1 |
| 2 |
| 1 |
| 2 |

Eξ=
| 3 |
| 2 |
点评:本题主要考查了相互独立事件的概率公式的运用,随机变量的分布列,数学期望,求解 的关键是要能对题目中较为复杂的事件进行分解,从而代入公式进行求解.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
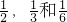 ,现在这3名工人独立从中任选一个项目参与建设.
,现在这3名工人独立从中任选一个项目参与建设.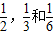 ,现在这3名工人独立从中任选一个项目参与建设.
,现在这3名工人独立从中任选一个项目参与建设.