题目内容
已知函数y=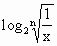 (n∈N).
(n∈N).
(Ⅰ)当n=1,2,3…时,把已知函数的图像和直线y=1的交点的横坐标依次记为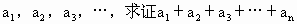 <1;
<1;
(Ⅱ)对于每一个n的值,设 为已知函数的图像上与x轴距离为1的两点,求证:n取任意一个正整数时,以
为已知函数的图像上与x轴距离为1的两点,求证:n取任意一个正整数时,以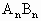 为直径的圆都与一条定直线相切,并求出这条定直线的方程和切点的坐标.
为直径的圆都与一条定直线相切,并求出这条定直线的方程和切点的坐标.
答案:
解析:
解析:
|
解:原函数可化为:y= (Ⅰ)y=1时,可求得x= ∴ ∴ (Ⅱ)同理可以求 因此 ∴以C为圆点、 由点C的纵坐标为0,可知从点C到y轴作垂线的垂足就是原点即切点,所以切点坐标为(0,0). |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
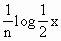
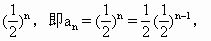
 为首项,
为首项,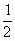 为公比的等比数列.
为公比的等比数列.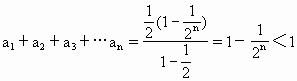
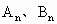 的横坐标,可得
的横坐标,可得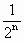 ,1)和(
,1)和( ,-1)
,-1)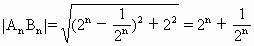

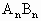 为直径的圆必与定直线y轴相切,这条定直线的方程为x=0.
为直径的圆必与定直线y轴相切,这条定直线的方程为x=0. B.7
B.7