Question

（本小题满分12分）

已知函数.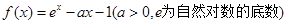

⑴求函数的最小值；

⑵若≥0对任意的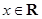恒成立，求实数a的值；

⑶在⑵的条件下，证明：.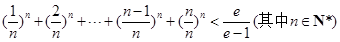

 

Answer 1

【答案】

解：（1）由题意，

由得.

当时, ；当时，.

∴在单调递减，在单调递增.

即在处取得极小值，且为最小值，

其最小值为                         （4分）

（2）对任意的恒成立，即在上，.

由（1），设，所以.

由得.

∴在区间上单调递增，在区间上单调递减，

∴在处取得极大值.

因此的解为，∴.                                     （8分）

（3）由（2）知，因为，所以对任意实数均有，即.

令 ，则.

∴.

∴

.                                  （12分）

【解析】略