题目内容
正四面体ABCD的棱长为1，平面α过棱AB,且CD∥α，则正四面体上的所有点在平面α内的射影构成的图形的面积是____________.
答案: 
解析:如图，
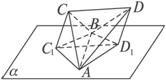
过C作C1C⊥α于C1点，过D作DD1⊥α于D1点.连结BC1、C1A、AD1、D1B，则AD1BC1为射影图形.
∵AB⊥CD,∴AB⊥C1D1.
∴S=
|AB|·|C1D1|.
∵CD∥α,∴C1D1=CD=1.
∴S=
×1×1=
.
练习册系列答案
阅读快车系列答案
相关题目
正四面体ABCD的棱长为1，G是△ABC的中心，M在线段DG上，且∠AMB=90°，则GM的长为（ ）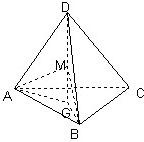
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2012•温州一模）如图，直线l⊥平面α，垂足为O，正四面体ABCD的棱长为4，C在平面α内，B是直线l上的动点，则当O到AD的距离为最大时，正四面体在平面α上的射影面积为（ ）