题目内容
函数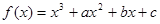 ,过曲线
,过曲线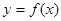 上的点P
上的点P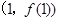 的切线方程为
的切线方程为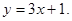
(1)若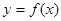 在
在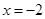 时有极值,求
时有极值,求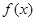 的表达式;
的表达式;
(2)在(1)的条件下,求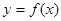 在[-3,1]上的最大值;
在[-3,1]上的最大值;
(3)若函数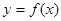 在区间[-2,1]上单调递增,求实数b的取值范围.
在区间[-2,1]上单调递增,求实数b的取值范围.
(1)
(2)最大值为13
(3))
解析试题分析:解:(1)由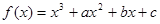 得
得 ,
,
过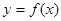 上点
上点 的切线方程为
的切线方程为 ,
,
即 .
.
而过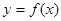 上点
上点 的切线方程为
的切线方程为 ,
,
故 3分
3分
∵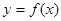 在
在 处有极值,故
处有极值,故
联立解得 . 5分
. 5分
(2)  ,令
,令 得
得 7分
7分
列下表:
因此,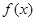 的极大值为
的极大值为 ,极小值为
,极小值为 ,
,
又 在
在 上的最大值为13.……10分
上的最大值为13.……10分
(3)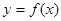 在
在 上单调递增,又
上单调递增,又 ,
,
由(1)知 ,依题意在
,依题意在 上恒有
上恒有 ,即
,即 即
即 在
在 上恒成立.当
上恒成立.当 时恒成立;当
时恒成立;当 时,
时, ,此时
,此时 ……12分
……12分
而 当且仅当
当且仅当 时成立
时成立
要使 恒成立,只须
恒成立,只须 .……14分
.……14分
考点:导数的运用
点评:主要是考查了导数在研究函数单调性中的运用,以及求解极值和最值的运用,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在
在 处取得极值。
处取得极值。 ;
;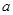 ,使得对任意
,使得对任意 ?若存在,求
?若存在,求 .
.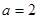 时,对任意
时,对任意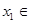 R,存在
R,存在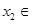 R,使
R,使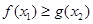 ,求实数
,求实数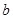 的取值范围;
的取值范围;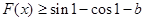 对任意
对任意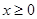 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (其中
(其中 ).
). 时,求函数
时,求函数 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最大值
上的最大值 .
.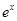 -ln(x+m).
-ln(x+m). (
( 为自然对数的底数)
为自然对数的底数) 在点
在点 处的切线平行于
处的切线平行于 轴,求
轴,求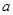 的值;
的值; 的极值;
的极值; 时,若直线
时,若直线 与曲线
与曲线 的最大值.
的最大值.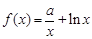 ,
,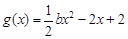 ,
,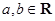
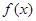 的单调区间;
的单调区间;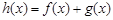 ,当
,当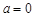 时,
时,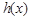 在
在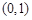 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数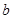 的取值范围;
的取值范围;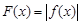 ,证明:存在一条过原点的直线
,证明:存在一条过原点的直线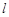 与
与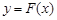 的图象有两个切点
的图象有两个切点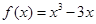
 的单调区间;
的单调区间;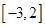 上的最值
上的最值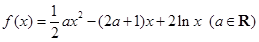 .
.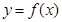 在
在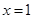 和
和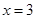 处的切线互相平行,求
处的切线互相平行,求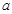 的值;
的值;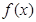 的单调区间;
的单调区间;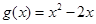 ,若对任意
,若对任意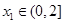 ,均存在
,均存在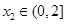 ,使得
,使得 ,求
,求