题目内容
函数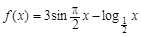 的图象与x轴交点的个数是
的图象与x轴交点的个数是
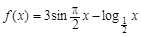 的图象与x轴交点的个数是
的图象与x轴交点的个数是| A.2 | B.3 | C.4 | D.5 |
D

分析:先把研究函数零点个数问题转化为对应的函数
 与
与 的交点个数,再利用函数的周期以及函数的最值以及单调性画出函数图象,由图即可得出结论.
的交点个数,再利用函数的周期以及函数的最值以及单调性画出函数图象,由图即可得出结论.解:因为函数
 的零点个数就是对应的函数
的零点个数就是对应的函数 与
与 的交点个数.
的交点个数.又因为函数
 的周期
的周期 .而
.而
在同一坐标系中画图得:
由图得:交点有5个.
故函数
 的零点个数是5.
的零点个数是5.故选 D.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
 的图象的一部分,A是图象与x轴的一个交点,B、C分别是图象上的一个最高点和一个最低点,且AB⊥AC,则ω的值为 ( )
的图象的一部分,A是图象与x轴的一个交点,B、C分别是图象上的一个最高点和一个最低点,且AB⊥AC,则ω的值为 ( ) D.
D.


 的取值范围为( )
的取值范围为( )



 ,则
,则
 .
.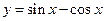 的图象可由
的图象可由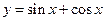 的图像向右平移( )
的图像向右平移( )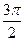 个单位
个单位
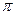 个单位
个单位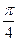 个单位
个单位 个单位
个单位 的部分图象如图所示
的部分图象如图所示
 的最小正周期及解析式;
的最小正周期及解析式; 求函数
求函数 在区间
在区间  上的最大值和最小值.
上的最大值和最小值.