题目内容
已知数列{an}为等差数列.(1)若a1=3,公差d=1,且a12+a2+a3+…+am≤48,求m的最大值;
(2)对于给定的正整数m,若a12+am+12=1,求S=am+1+am+2+…+a2m+1的最大值.
解:(1)由a12+a2+a3+…+am≤48,
可得a12-a1+a1+a2+a3+…+am≤48,又a1=3,d=1,
可得6+3m+![]() ≤48.
≤48.
整理得m2+5m-84≤0,
解得-12≤m≤7,即m的最大值为7.
(2)S=am+1+am+2+…+a2m+1=![]() ,
,
设am+1+a2m+1=A,
则A=am+1+a2m+1+a1-a1=am+1+2am+1-a1=3am+1-a1,
则am+1=![]() ,由a12+(
,由a12+(![]() )2=1,
)2=1,
可得10a12+2Aa1+A2-9=0,
由Δ=4A2-40(A2-9)≥0,
可得![]() ≤A≤
≤A≤![]() .
.
所以S=![]() =
=![]() ≤
≤![]() ,
,
即S的最大值为![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

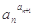 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4