题目内容
已知函数f(x)=2cos2x+2sinxcosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)的单调增区间.
解:(Ⅰ)f(x)=2cos2x+2sinxcosx=(2cos2x-1)+2sinxcosx+1=cos2x+sin2x+1= ,(4分)
,(4分)
∴f(x)的最小正周期 . (7分)
. (7分)
(Ⅱ)令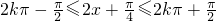 ,(10分) 解得
,(10分) 解得  ,(13分)
,(13分)
∴f(x)的单调增区间 . (14分)
. (14分)
分析:(Ⅰ)化简函数解析式为 ,利用周期公式求出f(x)的最小正周期.
,利用周期公式求出f(x)的最小正周期.
(Ⅱ)令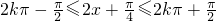 ,解得x的范围,即可得到f(x)的单调增区间.
,解得x的范围,即可得到f(x)的单调增区间.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的单调性,周期性及其求法,化简函数解析式为 ,是解题的关键.
,是解题的关键.
 ,(4分)
,(4分)∴f(x)的最小正周期
 . (7分)
. (7分)(Ⅱ)令
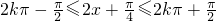 ,(10分) 解得
,(10分) 解得  ,(13分)
,(13分)∴f(x)的单调增区间
 . (14分)
. (14分)分析:(Ⅰ)化简函数解析式为
 ,利用周期公式求出f(x)的最小正周期.
,利用周期公式求出f(x)的最小正周期.(Ⅱ)令
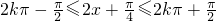 ,解得x的范围,即可得到f(x)的单调增区间.
,解得x的范围,即可得到f(x)的单调增区间.点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的单调性,周期性及其求法,化简函数解析式为
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目