题目内容
已知函数 =2
=2 -
- -
- sin2
sin2 +1
+1
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)当 时,若
时,若 ≥log2
≥log2 恒成立,求
恒成立,求  的取值范围.
的取值范围.
解:(Ⅰ)∵ 
 …………………………………………3分
…………………………………………3分
由 ,得
,得 ,…5分
,…5分
∴ f(x)的单调递增区间为  .…………6分
.…………6分
(或者:f(x) = —
— +2=
+2= cos2x—
cos2x— +2
+2
=— +2 …………………………………………………3分
+2 …………………………………………………3分
令  +2kπ≤
+2kπ≤ ≤
≤ +2kπ k∈Z
+2kπ k∈Z
则 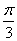 +kπ≤x≤
+kπ≤x≤ +kπ k∈Z ……………………………………5分
+kπ k∈Z ……………………………………5分
∴ f(x)的单调递增区间为:[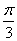 +kπ,
+kπ, +kπ] k∈Z …………6分)
+kπ] k∈Z …………6分)
(Ⅱ) ∵  , ∴
, ∴
 , ………………………………7分
, ………………………………7分
∴ —1≤cos( )≤—
)≤— ,
,  , …………8分
, …………8分
(或者:∵  ,∴
,∴ ……………………………………7分
……………………………………7分
∴  ≤
≤ ≤1 ∴ 1≤—
≤1 ∴ 1≤— +2 ≤
+2 ≤ …………8分)
…………8分)
∴  . …………………………………………9分
. …………………………………………9分
若f(x)≥log2t恒成立, 则 ∴log2t ≤1 ∴0<t≤2, ………11分
即t的取值范围为(0,2]. …………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 根据上述规律,第五个等式为__________________________.
根据上述规律,第五个等式为__________________________. .则
.则 .
. 的最小正周期为
的最小正周期为 ,则它的图像的一个对称中心为( )
,则它的图像的一个对称中心为( ) B.
B.  C.
C.  D.
D. 
 A.
A. B.
B. C.
C. D.
D.
 中,
中, 分别为三个内角
分别为三个内角 所对的边,设向量
所对的边,设向量 ,若向量
,若向量 ,则角
,则角 的大小为( )
的大小为( ) B.
B.  C.
C.  D.
D. 
 ,求直线l的方程;
,求直线l的方程;