Question

已知函数f（x）=（x﹣k）e^x．

（Ⅰ）求f（x）的单调区间；

（Ⅱ）求f（x）在区间[0，1]上的最小值．

Answer 1

考点：

利用导数研究函数的单调性；利用导数求闭区间上函数的最值．

专题：

计算题；综合题；分类讨论．

分析：

（I）求导，令导数等于零，解方程，跟据f′（x）f（x）随x的变化情况即可求出函数的单调区间；（Ⅱ）根据（I），对k﹣1是否在区间[0，1]内进行讨论，从而求得f（x）在区间[0，1]上的最小值．

解答：

解：（Ⅰ）f′（x）=（x﹣k+1）e^x，

令f′（x）=0，得x=k﹣1，

f′（x）f（x）随x的变化情况如下：

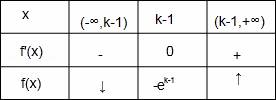
∴f（x）的单调递减区间是（﹣∞，k﹣1），f（x）的单调递增区间（k﹣1，+∞）；（Ⅱ）当k﹣1≤0，即k≤1时，函数f（x）在区间[0，1]上单调递增，

∴f（x）在区间[0，1]上的最小值为f（0）=﹣k；

当0＜k﹣1＜1，即1＜k＜2时，由（I）知，f（x）在区间[0，k﹣1]上单调递减，f（x）在区间（k﹣1，1]上单调递增，

∴f（x）在区间[0，1]上的最小值为f（k﹣1）=﹣e^k﹣1；

当k﹣1≥1，即k≥2时，函数f（x）在区间[0，1]上单调递减，

∴f（x）在区间[0，1]上的最小值为f（1）=（1﹣k）e；

综上所述f（x）_min=．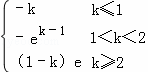

点评：

此题是个中档题．考查利用导数研究函数的单调性和在闭区间上的最值问题，对方程f'（x）=0根是否在区间[0，1]内进行讨论，体现了分类讨论的思想方法，增加了题目的难度．