Question

抛物线y²=4x上有两定点A、B分别在第一和第四象限,F为抛物线的焦点,且|AF|=2,|BF|=5,在抛物线AOB部分上求一点P,使△ABP的面积最大,并求出最大值.

Answer 1

解:抛物线y²=4x的焦点为F(1,0),准线方程为l:x=－1,

∵|AF|=2,∴x_A+1=2.∴x_A=1.

不妨设点A在第一象限,点B在第四象限,

则A点的坐标为(1,2),B点的坐标为(4,－4).∴|AB|=3,直线AB的方程为2x+y－4=0.

设P(,y₀)为抛物线AOB部分上一点,d为P到AB的距离,则－4＜y₀＜2,

d=,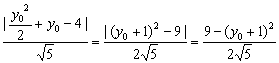

∴当y₀=－1时,d_max=,x₀=.

∴P点的坐标为(,－1).

∴△PAB的面积的最大值为.