题目内容
正方体ABCD-A1B1C1D1的棱长为1,E在棱CC1上,C1E=3CE,设平面A1DE与正方体的侧面BB1C1C交于线段EF,则线段EF的长为______.
∵E在棱CC1上,C1E=3CE,设平面A1DE与正方体的侧面BB1C1C交于线段EF,
∴EF是∥A1D,否则A1DEF就不是一个平面.
∵A1ADD1∥BB1C1C,而A1D和EF分别在这两个平面内,
要使得他们在同一平面内,只有平行时,否则为异面,
∴F在B1C1上,且C1F=3B1F,
∵正方体ABCD-A1B1C1D1的棱长为1,
∴C1E=C1F=
,
∴EF=
=
.
故答案为:
.

∴EF是∥A1D,否则A1DEF就不是一个平面.
∵A1ADD1∥BB1C1C,而A1D和EF分别在这两个平面内,
要使得他们在同一平面内,只有平行时,否则为异面,
∴F在B1C1上,且C1F=3B1F,
∵正方体ABCD-A1B1C1D1的棱长为1,
∴C1E=C1F=
| 3 |
| 4 |
∴EF=
|
| 3 |
| 4 |
| 2 |
故答案为:
| 3 |
| 4 |
| 2 |


练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
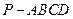 的底面
的底面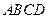 是半径为
是半径为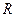 的圆的内接四边形,其中
的圆的内接四边形,其中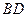 是圆的直径,
是圆的直径,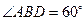 ,
,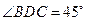 ,
,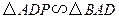 .
.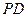 的长;
的长;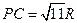 ,求三棱锥
,求三棱锥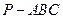 的体积.
的体积.