Question

为了了解某地区高三男性学生的身体发育情况,抽查了地区内100名高三男生的体重情况,结果如下(单位:kg).

56.5	69.5	65	61.5	64.5	66.5	64	64.5	76	58.5
72	73.5	56	67	70	57.5	65.5	68	71	75
62	68.5	62.5	66	59.5	63.5	64.5	67.5	73	68
55	72	66.5	74	63	60	55.5	70	64.5	58
64	70.5	57	62.5	68	69	71.5	73	62	58
76	71	66	63.5	56	59.5	63.5	65	70	74.5
68.5	64	55.5	72.5	66.5	68	76	57.5	60	71.5
57	69.5	74	64.5	59	61.5	67	68	63.5	58
59	65.5	62.5	69.5	72	64.5	75.5	68.5	64	62
65.5	58.5	67.5	70.5	65	66	66.5	70	63	59.5

    试根据上述数据画出样本的频率分布直方图,并对相应的总体分布作出估计.

Answer 1

思路分析：按照下列步骤获得样本的频率分布:

(1)求最大值与最小值的差.在上述数据中,最大值是76,最小值是55,极差是76-55=21.

(2)确定组距与组数.如果将组距定为2,那么由21÷2=10.5,组数为11,这个组数是适合的.于是组距为2,组数为11.

(3)决定分点.根据本例中数据的特点,第1小组的起点可取为54.5,第1小组的终点可取为56.5,为了避免一个数据既是起点,又是终点从而造成重复计算,我们规定分组的区间是“左闭右开”的.这样,所得到的分组是［54.5,56.5),［56.5,58.5),…,［74.5,76.5］.

(4)列频率分布表.

(5)绘制频率分布直方图.

解:频率分布表如下表:

分组	个数累计	频数	频率
［54.5,56.5)		2	0.02
［56.5,58.5)		6	0.06
［58.5,60.5)		10	0.10
［60.5,62.5)		10	0.10
［62.5,64.5)		14	0.14
［64.5,66.5)		16	0.16
［66.5,68.5)		13	0.13
［68.5,70.5)		11	0.11
［70.5,72.5)		8	0.08
［72.5,74.5)		7	0.07
［74.5,76.5)		3	0.03
合计	100	100	1.00

频率分布直方图如图2-2-7所示.

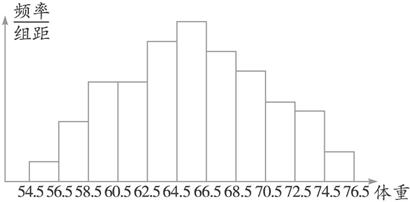
图2-2-7

    根据频率分布直方图,我们可以估计,体重在(64.5,66.5) kg的学生最多,约占学生总数的16%;体重小于58.5 kg的学生较少,约占8%，整体分布是大致对称的.