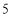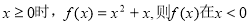题目内容
求半径为 ,圆心在直线
,圆心在直线 :
: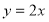 上,且被直线
上,且被直线 :
: 所截弦的长为
所截弦的长为 的圆的方程.
的圆的方程.
圆的方程为: 和
和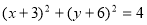 .
.
【解析】
试题分析:由圆心在直线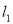 :
: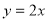 上,设出圆心C的坐标为
上,设出圆心C的坐标为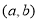 ,则
,则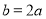 ,又圆的半径为2,且被直线
,又圆的半径为2,且被直线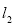 :
: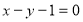 所截弦的长为
所截弦的长为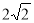 ,利用点到直线的距离公式表示出圆心到直线
,利用点到直线的距离公式表示出圆心到直线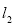 :
: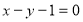 的距离
的距离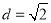 ,解得到
,解得到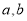 的值,进而确定出圆心C的坐标,由圆心和半径写出圆的方程即可.
的值,进而确定出圆心C的坐标,由圆心和半径写出圆的方程即可.
试题解析:.【解析】
设所求圆的圆心为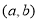 ,
,
则圆心到直线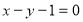 的距离
的距离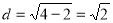
根据题意有:
 解方程组得:
解方程组得: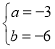 ,
,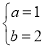
所以,所求的圆的方程为: 和
和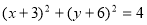
(或 和
和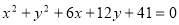 ) (12分)
) (12分)
考点:本题考查直线与圆相交的性质、圆的标准方程、点到直线的距离公式,当直线与圆相交时,由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某射击俱乐部四名运动员甲、乙、丙、丁在选拔赛 中所得的平均环数 及其方差
及其方差 如表所示,若从中选送一人参加决赛,则最佳人选是
如表所示,若从中选送一人参加决赛,则最佳人选是
| 甲 | 乙 | 丙 | 丁 |
| 9.1 | 9.3 | 9.3 | 9.2 |
| 5.7 | 6.2 | 5.7 | 6.4 |
A.甲 B.乙
C.丙 D.丁