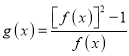Question

【题目】已知点，圆

（1）过点的圆的切线只有一条，求的值及切线方程；

（2）若过点且在两坐标轴上截距相等的直线被圆截得的弦长为，求的值.

Answer 1

【答案】(1) 时，切线方程为x＋y－4＝0，) 时，切线方程为x－y－4＝0(2)

【解析】试题分析：若过点A的圆的切线只有一条，说明点在圆上，点A的坐标满足圆的方程求出；由于直线在两坐标轴上的截距相等，所以可用直线的截距式巧设直线的方程；求圆的弦长，一般先求出圆心到直线的距离，然后利用勾股定理计算弦长，利用待定系数法，列方程，解方程组求出.

试题解析：(1)由于过点A的圆的切线只有一条，则点A在圆上，故12＋a2＝4，∴a＝±.

当a＝时，A(1， )，切线方程为x＋y－4＝0；

当a＝－时，A(1，－ )，切线方程为x－y－4＝0，

∴a＝时，切线方程为x＋y－4＝0，

a＝－时，切线方程为x－y－4＝0.

(2)设直线方程为 x＋y＝b，

由于直线过点A，∴1＋a＝b，a＝b－1.

又圆心到直线的距离d＝，

∴()2＋()2＝4.

∴b＝± .∴a＝±－1.