题目内容
(江苏卷21④)已知实数a,b≥0,求证: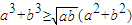
【答案】分析:方法一,比较法;作差--变形--判断符号,应用实数a,b≥0,(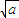 -
-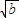 )2≥0
)2≥0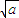
方法二,比较法;作差--变形--判断符号,应用实数a,b≥0,当a>b时,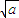 >
>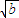 ,
,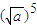 >
>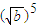 ,当a<b时,
,当a<b时,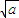 <
<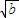 ,
,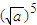 <
<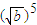 .
.
解答:(方法一)证明:a3+b3-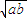 (a2+b2)=a2
(a2+b2)=a2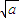 (
(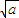 -
-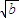 )+b2
)+b2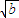 (
(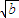 -
-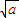 )
)
=(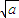 -
-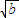 )[(
)[(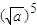 -
-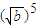 ]①
]①
=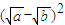 [
[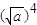 +
+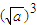 (
(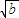 )+
)+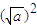
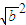 )+
)+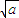
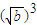 +
+ ]
]
因为实数a、b≥0,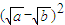 ≥0,
≥0,
[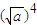 +
+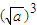 (
(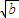 )+
)+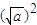
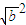 )+
)+
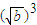 +
+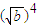 ]≥0
]≥0
所以,上式①≥0.
即有: .
.
(方法二)证明:由a、b是非负实数,作差得明:
a3+b3- (a2+b2)=a2
(a2+b2)=a2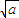 (
(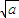 -
- )+b2
)+b2 (
( -
-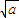 )
)
=(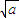 -
-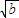 )[(
)[(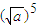 -
-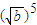 ]①
]①
当a>b时,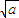 >
>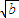 ,从而
,从而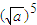 -
-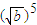 >0,得 (
>0,得 (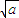 -
-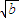 )[(
)[(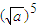 -
- ]≥0;
]≥0;
当 当a<b时,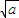 <
<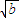 ,从而
,从而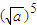 -
-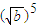 <0,得(
<0,得(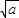 -
-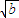 )[(
)[(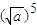 -
-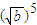 ]≥0;
]≥0;
所以,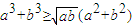 .
.
点评:本题主要考查证明不等式的基本方法,考查推理论证的能力
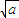 -
-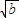 )2≥0
)2≥0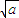
方法二,比较法;作差--变形--判断符号,应用实数a,b≥0,当a>b时,
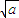 >
>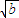 ,
,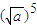 >
>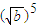 ,当a<b时,
,当a<b时,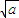 <
<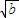 ,
,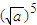 <
<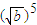 .
.解答:(方法一)证明:a3+b3-
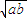 (a2+b2)=a2
(a2+b2)=a2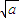 (
(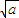 -
-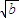 )+b2
)+b2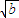 (
(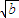 -
-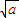 )
)=(
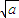 -
-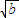 )[(
)[(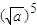 -
-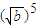 ]①
]①=
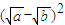 [
[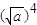 +
+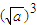 (
(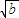 )+
)+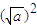
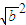 )+
)+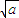
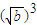 +
+ ]
]因为实数a、b≥0,
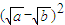 ≥0,
≥0,[
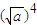 +
+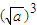 (
(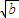 )+
)+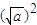
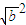 )+
)+
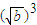 +
+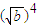 ]≥0
]≥0所以,上式①≥0.
即有:
 .
.(方法二)证明:由a、b是非负实数,作差得明:
a3+b3-
 (a2+b2)=a2
(a2+b2)=a2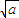 (
(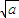 -
- )+b2
)+b2 (
( -
-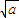 )
)=(
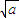 -
-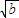 )[(
)[(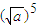 -
-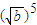 ]①
]①当a>b时,
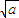 >
>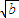 ,从而
,从而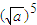 -
-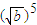 >0,得 (
>0,得 (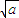 -
-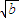 )[(
)[(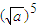 -
- ]≥0;
]≥0;当 当a<b时,
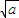 <
<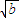 ,从而
,从而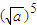 -
-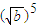 <0,得(
<0,得(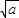 -
-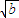 )[(
)[(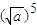 -
-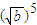 ]≥0;
]≥0;所以,
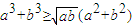 .
.点评:本题主要考查证明不等式的基本方法,考查推理论证的能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目