Question

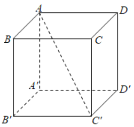
【题目】在正方体中,若点(异于点)是棱上一点,则满足与所成的角为的点的个数为（ ）

A.0B.3C.4D.6

Answer 1

【答案】B

【解析】

建立空间直角坐标系，通过分类讨论利用异面直线的方向向量所成的夹角即可找出所有满足条件的点的个数．

建立如图所示的空间直角坐标系，

不妨设棱长，，0，，，1，．

①在△中，，因此．

同理，与所成的角都为．

故当点位于（分别与上述棱平行或重合）棱，，上时，与所成的角都为，不满足条件；

②当点位于棱上时，设，，，，则，，，，1，．

若满足与所成的角为，则，

化为，无正数解，舍去；

同理，当点位于棱上时，也不符合条件；

③当点位于棱上时，设，，，，

则，，，，1，．

若满足与所成的角为，则，

化为，

，解得，满足条件，此时点．

④同理可求得棱上一点，棱上一点．

而其它棱上没有满足条件的点．

综上可知：满足条件的点有且只有3个．

故选：