题目内容
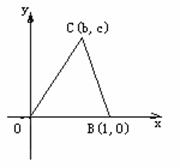
(21)已知O(0,0),B(1,0),C(b,c)是△OBC的三个顶点.(Ⅰ)写出△OBC的重心G,外心F,垂心H的坐标,并证明G,F,H三点共线;
(Ⅱ)当直线FH与OB平行时,求顶点C的轨迹.
(21)本小题主要考查直线与椭圆等基本知识,考查分析问题和解决问题的能力.
(Ⅰ)解:由△OBC三顶点坐标O(0,0),B(1,0),C(b,c)(c≠0),可求得
重心G(![]() ,
,![]() ),外心F(
),外心F(![]() ,
,![]() ),垂心H(b,
),垂心H(b,![]() )
)
当b=![]() 时,G、F、H三点的横坐标均为
时,G、F、H三点的横坐标均为![]() ,故三点共线;
,故三点共线;
当b≠![]() 时,设G、H所在直线的斜率为kGH,F、G所在直线的斜率为kFG.
时,设G、H所在直线的斜率为kGH,F、G所在直线的斜率为kFG.
因为kGH=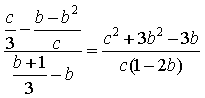
kFG=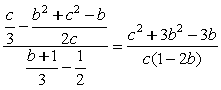
所以kGH=kFG,G、F、H三点共线
综上可得,G、F、H三点共线.
(Ⅱ)解:若FH∥OB,由kFH=![]() =0,得3(b2-b)+c2=0(c≠0,b≠
=0,得3(b2-b)+c2=0(c≠0,b≠![]() ),
),
配方得3(b-![]() )2+c2=
)2+c2=![]() ,
,
即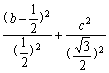 =1.
=1.
即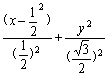 =1(x≠
=1(x≠![]() ,y≠0)
,y≠0)
因此,顶点C的轨迹是中心在(![]() ,0),长半轴长为
,0),长半轴长为![]() ,短半轴长为
,短半轴长为![]() ,且短轴在x轴上的椭圆,
,且短轴在x轴上的椭圆,
除去(0,0),(1,0),(![]() ,
,![]() ),(
),(![]() ,-
,-![]() )四点.
)四点.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
