题目内容
在某海滨城市附近海面有一台风.据监测，当前台风中心位于城市O(如下图)的东偏南θ(cosθ=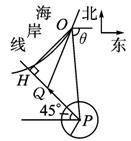
)方向300 km的海面P处，并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域，当前半径为60 km，并以10 km/h的速度不断增大.问几小时后该城市开始受到台风的侵袭？
解：设t小时后该城市开始受到台风影响，此时台风中心为Q,则PQ=20t,OQ=60+10t.
过O作PQ的垂线，垂足为H,则∠HPO=θ-45°.
由余弦定理得
OQ2=PQ2+PQ2-2PQ·PO·cos(θ-45°),
即(60+10t)2=400t2+90 000-2×20t×300cos(θ-45°).
∵cos(θ-45°)=cos(arccos
-)
=
·
+
·
=
∴t2-36t+288=0
解得t=12或24
当t=12时，台风开始侵袭这座城市；当t=24时，是台风侵袭这座城市的最后一刻.
所以，12小时后该城市开始受到台风的侵袭.
练习册系列答案
相关题目
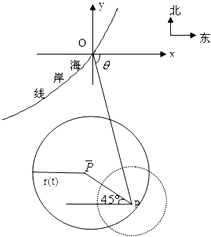在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南
在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南 
方向300km的海面P处，并以20km/h的速度向西偏北
方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？
)方向300 km的海面P处，并以20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域，当前半径为60 km,并以10 km/h的速度不断增大.问几小时后该城市开始受到台风的侵袭？
方向300 km的海面P处，并以20 km
/ h的速度向西偏北
的方向移动，台风侵袭的范围为圆形区域，当前半径为60 km ，并以10 km / h的速度不断增加，问几小时后该城市开始受到台风的侵袭？持续多长时间？