题目内容
17.已知f(x)是R上的奇函数,f(x)=$\left\{\begin{array}{l}{x^2}+2x(x≥0)\\-{x^2}+mx(x<0)\end{array}\right.$,则f(x-1)<f(mx)解集为(-1,+∞).分析 先根据f(x)为奇函数,便有f(-1)=-f(1),所以可求出m=2,所以f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x}&{x≥0}\\{-{x}^{2}+mx}&{x<0}\end{array}\right.$,而根据二次函数的单调性以及分段函数单调性的判断方法可得出函数f(x)在R上单调递增.所以由f(x-1)<f(2x)便得到x-1<2x,这样便解得x>-1.
解答 解:f(x)是R上的奇函数;
∴f(-1)=-f(1);
∴-1-m=-3;
∴m=2;
容易判断二次函数x2+2x在[0,+∞)单调递增,-x2+2x在(-∞,0)上单调递增;
∴x2+2x≥0,-x2+2x<0;
∴函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x}&{x≥0}\\{-{x}^{2}+2x}&{x<0}\end{array}\right.$在R上单调递增;
∴由f(x-1)<f(2x)得,x-1<2x;
∴x>-1;
∴f(x-1)<f(mx)的解集为(-1,+∞).
故答案为:(-1,+∞).
点评 考查奇函数的定义,二次函数的单调性,以及分段函数单调性的判断方法,函数单调性定义的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若sinθ+cosθ=$\frac{\sqrt{5}}{5}$,θ∈[0,π],则tanθ=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
7.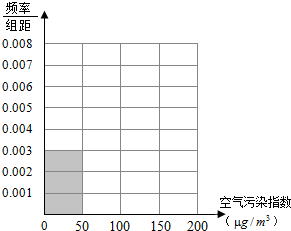 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
(Ⅱ)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
 春节期间,某校高二学生随交警对某高速公路某路段上行驶的七座以下小型汽车进行监控抽查,抽查方式按进入该路段的先后梅间隔20辆就抽取一辆的方法进行,共抽取了40辆,将它们的车速(km/h)分成6段区间:(70,80],(80,90],(90,100],(100,110],(110,120],(120,130],后得到如图的频率分布直方图.已知该段高速公路的规定时速为100km/h,超过规定时速将被罚款,规定如下:超过规定时速10%以内(含),不罚款;超过规定时速10%以上未超过20%的,处以50元罚款;超过规定时速20%以上未超过50%的,处以200元罚款.
春节期间,某校高二学生随交警对某高速公路某路段上行驶的七座以下小型汽车进行监控抽查,抽查方式按进入该路段的先后梅间隔20辆就抽取一辆的方法进行,共抽取了40辆,将它们的车速(km/h)分成6段区间:(70,80],(80,90],(90,100],(100,110],(110,120],(120,130],后得到如图的频率分布直方图.已知该段高速公路的规定时速为100km/h,超过规定时速将被罚款,规定如下:超过规定时速10%以内(含),不罚款;超过规定时速10%以上未超过20%的,处以50元罚款;超过规定时速20%以上未超过50%的,处以200元罚款.