题目内容
设f(x)=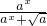 (a>0,a≠1),则f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)=________.
(a>0,a≠1),则f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)=________.
2010
分析:由f(x)=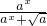 (a>0,a≠1),知f(1-x)+f(x)=
(a>0,a≠1),知f(1-x)+f(x)=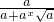 +
+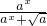 =1.由此能求出f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)的值.
=1.由此能求出f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)的值.
解答:∵f(x)=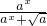 (a>0,a≠1),
(a>0,a≠1),
∴f(1-x)=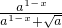 =
=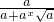 ,
,
∴f(1-x)+f(x)=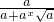 +
+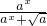
=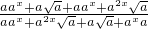
=1.
∴f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)
=[f(-2009)+f(2010)]+[f(-2008)+f(2009)]+…+[f(-1)+f(2)]+[f(0)+f(1)]
=1+1+…+1+1
=2010.
故答案为:2010.
点评:本题考查函数值的求法,解题时要认真审题,注意寻找规律.正确解题的关键是利用题设条件判断出f(1-x)+f(x)=1.
分析:由f(x)=
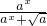 (a>0,a≠1),知f(1-x)+f(x)=
(a>0,a≠1),知f(1-x)+f(x)=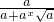 +
+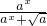 =1.由此能求出f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)的值.
=1.由此能求出f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)的值.解答:∵f(x)=
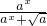 (a>0,a≠1),
(a>0,a≠1),∴f(1-x)=
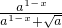 =
=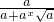 ,
,∴f(1-x)+f(x)=
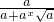 +
+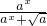
=
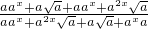
=1.
∴f(-2009)+f(-2008)+…+f(0)+f(1)+…+f(2010)
=[f(-2009)+f(2010)]+[f(-2008)+f(2009)]+…+[f(-1)+f(2)]+[f(0)+f(1)]
=1+1+…+1+1
=2010.
故答案为:2010.
点评:本题考查函数值的求法,解题时要认真审题,注意寻找规律.正确解题的关键是利用题设条件判断出f(1-x)+f(x)=1.

练习册系列答案
相关题目
