题目内容
设函数 ,区间M=[-1,1],集合N={y|y=f(x),x∈M},则使M=N成立的实数m的个数为
,区间M=[-1,1],集合N={y|y=f(x),x∈M},则使M=N成立的实数m的个数为
- A.1
- B.2
- C.3
- D.无数
B
分析:先判断函数f(x)是奇函数,题意可得,当-1≤x≤1时,函数的值域为[-1,1].分m>0和m<0 两种情况,分别利用函数的单调性求得m的值,综合可得结论.
解答:由函数 可得f(-x)=
可得f(-x)= =-
=- =-f(x),故函数f(x)是奇函数.
=-f(x),故函数f(x)是奇函数.
题意可得,当-1≤x≤1时,函数的值域为[-1,1].
①若x∈[0,1],且m>0,由 f(x)= =m-
=m- ,故函数在[0,1]上是增函数,故函数f(x)在区间M=[-1,1]上是增函数,
,故函数在[0,1]上是增函数,故函数f(x)在区间M=[-1,1]上是增函数,
故有f(-1)=-1,f(1)=1,即 =-1,
=-1, =1,解得 m=2.
=1,解得 m=2.
②若x∈[0,1],且m<0,由 f(x)= =m-
=m- ,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,
,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,
故有f(-1)=1,f(1)=-1,即 =1,
=1, =-1,解得 m=-2.
=-1,解得 m=-2.
③显然,m=0不满足条件.
综上可得,m=±2,故使M=N成立的实数m的个数为2,
故选B.
点评:本题主要考查集合关系中参数的取值范围问题,函数的奇偶性、单调性的应用,体现了分类讨论的数学思想,属于基础题.
分析:先判断函数f(x)是奇函数,题意可得,当-1≤x≤1时,函数的值域为[-1,1].分m>0和m<0 两种情况,分别利用函数的单调性求得m的值,综合可得结论.
解答:由函数
 可得f(-x)=
可得f(-x)= =-
=- =-f(x),故函数f(x)是奇函数.
=-f(x),故函数f(x)是奇函数.题意可得,当-1≤x≤1时,函数的值域为[-1,1].
①若x∈[0,1],且m>0,由 f(x)=
 =m-
=m- ,故函数在[0,1]上是增函数,故函数f(x)在区间M=[-1,1]上是增函数,
,故函数在[0,1]上是增函数,故函数f(x)在区间M=[-1,1]上是增函数,故有f(-1)=-1,f(1)=1,即
 =-1,
=-1, =1,解得 m=2.
=1,解得 m=2.②若x∈[0,1],且m<0,由 f(x)=
 =m-
=m- ,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,
,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,故有f(-1)=1,f(1)=-1,即
 =1,
=1, =-1,解得 m=-2.
=-1,解得 m=-2.③显然,m=0不满足条件.
综上可得,m=±2,故使M=N成立的实数m的个数为2,
故选B.
点评:本题主要考查集合关系中参数的取值范围问题,函数的奇偶性、单调性的应用,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 ,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个.
,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个. ,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个.
,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个. ,区间M=[a,b](其中a<b),集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有( )
,区间M=[a,b](其中a<b),集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有( ) ,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个.
,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个.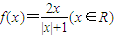 ,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个.
,区间M=[a,b](其中a<b)集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有 个.