题目内容
设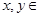 R,向量
R,向量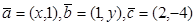 且
且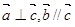 ,则
,则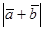 ( )
( )
A.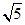 | B. | C.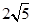 | D.10 |
B
解析试题分析:因为 ,所以
,所以 ;因为
;因为 ,所以
,所以 所以
所以 ,所以
,所以 。
。
考点:向量的模;平面向量垂直的条件;平面向量平行的条件。
点评:熟记且灵活应用性质:向量的平方就等于其模的平方。这条性质在求向量的模的时候经常用到。属于基础题型。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
已知△ABC, , 则△ABC的面积为( )
, 则△ABC的面积为( )
| A.1 | B.2 | C.3 | D.4 |
已知向量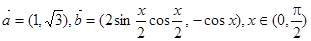 ,若
,若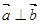 ,则
,则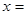
A.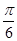 | B.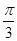 | C.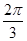 | D.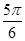 |
已知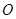 为平面上的定点,
为平面上的定点,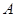 、
、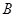 、
、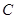 是平面上不共线的三点,若
是平面上不共线的三点,若
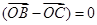 ,则DABC是( )
,则DABC是( )
| A.以AB为底边的等腰三角形 | B.以BC为底边的等腰三角形 |
| C.以AB为斜边的直角三角形 | D.以BC为斜边的直角三角形 |
已知 ,
, ,若
,若 ,则
,则 ( )
( )
A. | B. | C. | D. |
在空间直角坐标系中,若向量 ,则它们之间的关系是( )
,则它们之间的关系是( )
A. | B.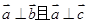 | C. | D. |
已知平面向量 ,且
,且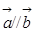 ,则
,则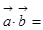 ( )
( )
| A.-30 | B.20 | C.15 | D.0 |
已知向量 ,
, ,若
,若 ∥
∥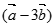 ,则实数k的取值为( )
,则实数k的取值为( )
A. | B. | C. | D. . . |
已知向量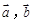 满足
满足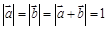 ,则向量
,则向量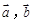 夹角的余弦值为( )
夹角的余弦值为( )
A.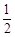 | B. | C.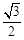 | D.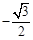 |