题目内容
如图, 已知边长为2的的菱形 与菱形
与菱形 全等,且
全等,且 ,平面
,平面 平面
平面 ,点
,点 为
为 的中点.
的中点.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(Ⅰ)见解析;(Ⅱ)见解析; (Ⅲ)
【解析】
试题分析:(Ⅰ)要证明线面平行,只需证明这条直线以平面内的一条直线平行即可,连结 ,易得
,易得 为三角形
为三角形 的中位线,所以,
的中位线,所以, ,
,
 平面
平面 ;要证明线线垂直,一般通过线面垂直得到,易得
;要证明线线垂直,一般通过线面垂直得到,易得 平面
平面 ,
,

 ,在菱形
,在菱形 中
中 ,
,
 平面
平面


(Ⅲ)利用等体积法即可,即
试题解析:(Ⅰ)连结 , ..1分
, ..1分
因为四边形 是菱形,
是菱形,
所以, ,又
,又 ,
,
所以, 为三角形
为三角形 的中位线 .2分
的中位线 .2分
所以, .
.
又
 平面
平面 ,
,
 平面
平面

 平面
平面 4分
4分
(Ⅱ)因为四边形 是菱形,所以
是菱形,所以 。
。
又平面 平面
平面 ,且交线为
,且交线为

 平面
平面 , 2分
, 2分
又

 平面
平面


 3分
3分
 在菱形
在菱形 中,
中, ,
,

 4分
4分

 平面
平面

 平面
平面 5分
5分

 6分
6分
(Ⅲ)由题知, =2,故
=2,故 ,
,
在三角形 中,
中, ,
, ,所以
,所以 =
= . 1分
. 1分
又 ,所以
,所以 ,所以
,所以 是等边三角形,
是等边三角形,
所以 ,
,
所以 2分
2分
又 面
面 ,所以,点C到面
,所以,点C到面 的距离
的距离 3分
3分
所以  4分
4分
考点:立体几何的综合应用

练习册系列答案
相关题目
 满足约束条件
满足约束条件 ,则
,则 的最大值是( )
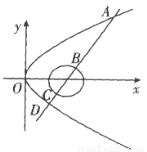
的最大值是( )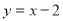 与圆
与圆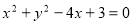 及抛物线
及抛物线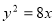 依次交于A、B、C、D四点,则
依次交于A、B、C、D四点,则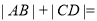 ( )
( )
 ),可得这个几何体的体积是__________
),可得这个几何体的体积是__________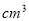 .
.
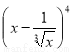 的展开式中常数项为A,则A=
的展开式中常数项为A,则A= :
: ,在圆M上随机取一点P,则P到直线
,在圆M上随机取一点P,则P到直线 的距离大于
的距离大于 的概率为 .
的概率为 .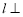 平面
平面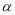 ,直线
,直线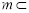 平面
平面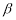 ,有下列四个命题:①若
,有下列四个命题:①若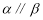 ,则
,则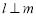 ;
;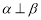 ,则
,则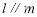 ;③若
;③若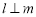 ,则
,则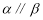 .
. :命题
:命题 .则下列判断正确的是
.则下列判断正确的是 是真命题
是真命题  是真命题
是真命题 中,若双曲线的渐近线方程是
中,若双曲线的渐近线方程是 ,且经过点
,且经过点 ,则该双曲线的方程是 .
,则该双曲线的方程是 .