题目内容
给出以下四个命题:①若cosαcosβ=1,则sin(α+β)=0;②已知直线x=m与函数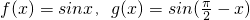 的图象分别交于点M,N,则|MN|的最大值为
的图象分别交于点M,N,则|MN|的最大值为 ;③若数列an=n2+λn(n∈N+)为单调递增数列,则λ取值范围是λ<-2;④已知数列an的通项
;③若数列an=n2+λn(n∈N+)为单调递增数列,则λ取值范围是λ<-2;④已知数列an的通项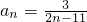 ,其前n项和为Sn,则使Sn>0的n的最小值为12.其中正确命题的序号为________.
,其前n项和为Sn,则使Sn>0的n的最小值为12.其中正确命题的序号为________.
①②
分析:①若cosαcosβ=1,可知,α、β两角的同时在x轴正半轴或者在负半轴上,有此则可得sin(α+β)=0;
②已知直线x=m与函数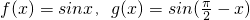 的图象分别交于点M,N,则|MN|的最大值为
的图象分别交于点M,N,则|MN|的最大值为 ,f(x)-g(x)的最大值即为|MN|的最大值,验证即可;
,f(x)-g(x)的最大值即为|MN|的最大值,验证即可;
③若数列an=n2+λn(n∈N+)为单调递增数列,则λ取值范围是λ<-2,由二次函数的性质及数列的离散性特征转化出参数所满足的不等式即可;
④已知数列an的通项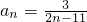 ,其前n项和为Sn,则使Sn>0的n的最小值为12,研究数列的前11项的值即可得出结论.
,其前n项和为Sn,则使Sn>0的n的最小值为12,研究数列的前11项的值即可得出结论.
解答:①若cosαcosβ=1,则α、β两角的同时在x轴正半轴或者在负半轴上,故sin(α+β)=0,此命题正确;
②已知直线x=m与函数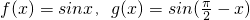 的图象分别交于点M,N,则|MN|的最大值为
的图象分别交于点M,N,则|MN|的最大值为 ,由于|MN|=|f(x)-g(x)|=|sinx-cosx|=|
,由于|MN|=|f(x)-g(x)|=|sinx-cosx|=| sin(x-
sin(x- )|
)| ,此命题正确;
,此命题正确;
③若数列an=n2+λn(n∈N+)为单调递增数列,则λ取值范围是λ<-2,由二次函数的性质及数列的特征得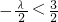 ,即λ>-3,故此命题不对;
,即λ>-3,故此命题不对;
④已知数列an的通项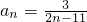 ,其前n项和为Sn,则使Sn>0的n的最小值为12,数列前十一项的值分别为-
,其前n项和为Sn,则使Sn>0的n的最小值为12,数列前十一项的值分别为- ,
,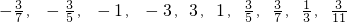 ,故S11>0,使Sn>0的n的最小值为11,此命题错误.
,故S11>0,使Sn>0的n的最小值为11,此命题错误.
故答案为①②
点评:本题考查数列与函数的关系,数列的最值,三角函数的最值等,涉及到的知识点较多,判断较繁.
分析:①若cosαcosβ=1,可知,α、β两角的同时在x轴正半轴或者在负半轴上,有此则可得sin(α+β)=0;
②已知直线x=m与函数
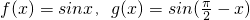 的图象分别交于点M,N,则|MN|的最大值为
的图象分别交于点M,N,则|MN|的最大值为 ,f(x)-g(x)的最大值即为|MN|的最大值,验证即可;
,f(x)-g(x)的最大值即为|MN|的最大值,验证即可;③若数列an=n2+λn(n∈N+)为单调递增数列,则λ取值范围是λ<-2,由二次函数的性质及数列的离散性特征转化出参数所满足的不等式即可;
④已知数列an的通项
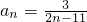 ,其前n项和为Sn,则使Sn>0的n的最小值为12,研究数列的前11项的值即可得出结论.
,其前n项和为Sn,则使Sn>0的n的最小值为12,研究数列的前11项的值即可得出结论.解答:①若cosαcosβ=1,则α、β两角的同时在x轴正半轴或者在负半轴上,故sin(α+β)=0,此命题正确;
②已知直线x=m与函数
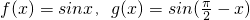 的图象分别交于点M,N,则|MN|的最大值为
的图象分别交于点M,N,则|MN|的最大值为 ,由于|MN|=|f(x)-g(x)|=|sinx-cosx|=|
,由于|MN|=|f(x)-g(x)|=|sinx-cosx|=| sin(x-
sin(x- )|
)| ,此命题正确;
,此命题正确;③若数列an=n2+λn(n∈N+)为单调递增数列,则λ取值范围是λ<-2,由二次函数的性质及数列的特征得
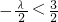 ,即λ>-3,故此命题不对;
,即λ>-3,故此命题不对;④已知数列an的通项
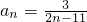 ,其前n项和为Sn,则使Sn>0的n的最小值为12,数列前十一项的值分别为-
,其前n项和为Sn,则使Sn>0的n的最小值为12,数列前十一项的值分别为- ,
,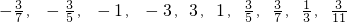 ,故S11>0,使Sn>0的n的最小值为11,此命题错误.
,故S11>0,使Sn>0的n的最小值为11,此命题错误.故答案为①②
点评:本题考查数列与函数的关系,数列的最值,三角函数的最值等,涉及到的知识点较多,判断较繁.

练习册系列答案
相关题目
定义平面向量之间的一种运算“*”如下:对任意的
=(m,n),
=(p,q),令
*
=mq-np.给出以下四个命题:(1)若
与
共线,则
*
=0;(2)
*
=
*
;(3)对任意的λ∈R,有(λ
)*
=λ(
*
)(4)(
*
)2+(
•
)2=|
|2•|
|2.(注:这里
•
指
与
的数量积)则其中所有真命题的序号是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、(1)(2)(3) |
| B、(2)(3)(4) |
| C、(1)(3)(4) |
| D、(1)(2)(4) |
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈[0,1],给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈[0,1],给出以下四个命题: