题目内容
 如图,过点P(7,0)作直线l与圆O:x2+y2=25交于A,B两点,若PA=3,则直线l的方程为
如图,过点P(7,0)作直线l与圆O:x2+y2=25交于A,B两点,若PA=3,则直线l的方程为5
x±11y-35
=0
| 3 |
| 3 |
5
x±11y-35
=0
.| 3 |
| 3 |
分析:过P作圆O的切线PQ,根据勾股定理求出PQ的长,再利用切割线定理求出PB的长,由PB-PA求出AB的长,利用垂径定理得到C为AB中点,求出AC的长,再利用勾股定理求出OC的长,即为圆心O到直线AB的距离,设直线AB解析式为y=k(x-7),利用点到直线的距离公式列出关于k的方程,求出方程的解得到k的值,即可确定出直线l方程.
解答: 解:如图,过P作圆O的切线PQ,可得OQ⊥PQ,利用勾股定理得:PQ=
解:如图,过P作圆O的切线PQ,可得OQ⊥PQ,利用勾股定理得:PQ=
=2
,
∵PA=3,∴PB=
=8,即AB=PB-PA=5,
∴AC=
,
根据勾股定理得:OC=
,
设直线l解析式为y=k(x-7),即kx-y-7k=0,
∴
=
,
解得:k=±
,
则直线l方程为5
x±11y-35
=0.
故答案为:5
x±11y-35
=0
 解:如图,过P作圆O的切线PQ,可得OQ⊥PQ,利用勾股定理得:PQ=
解:如图,过P作圆O的切线PQ,可得OQ⊥PQ,利用勾股定理得:PQ=| OP2-OQ2 |
| 6 |
∵PA=3,∴PB=
| PQ2 |
| PA |
∴AC=
| 5 |
| 2 |
根据勾股定理得:OC=
5
| ||
| 2 |
设直线l解析式为y=k(x-7),即kx-y-7k=0,
∴
| |-7k| | ||
|
5
| ||
| 2 |
解得:k=±
5
| ||
| 11 |
则直线l方程为5
| 3 |
| 3 |
故答案为:5
| 3 |
| 3 |
点评:此题考查了直线与圆的位置关系,涉及的知识有:切割线定理,垂径定理,勾股定理,点到直线的距离公式,以及直线的点斜式方程,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y
已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y 如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.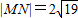 时,求直线l的方程.
时,求直线l的方程.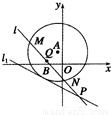
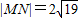 时,求直线l的方程.
时,求直线l的方程.