题目内容

函数f（x）=x²与函数g（x）=x的图象所围成的封闭图形的面积为

1

6

1

6

．

分析：联立

y=x

y=x2

，求其交点坐标，再利用定积分求出即可．

解答：解：联立

y=x

y=x2

，解得

x=0

y=0

，或

x=1

y=1

，即函数f（x）=x²与函数g（x）=x的图象的交点（0，0），（1，1）．
于是所求的面积=

∫

1

0

(x-x2)dx=(

x2

2

-

x3

3

)

|

1

0

=

1

2

-

1

3

=

1

6

．
故答案为

1

6

．

点评：利用定积分求封闭图形的面积是求面积的通法，应熟练掌握．

练习册系列答案

小学课时特训系列答案

1加1轻巧夺冠小专家课时练练通系列答案

校缘自助课堂系列答案

新编每课一练系列答案

超能学典小学生一卷通系列答案

浙江期末全真卷系列答案

练习册长春出版社系列答案

语文活页系列答案

优质课堂导学案系列答案

优品新课堂系列答案

相关题目

定义：两个连续函数（图象不间断）f（x），g（x）在区间[a，b]上都有意义，我们称函数|f（x）+g（x）|在[a，b]上的最大值叫做函数f（x）与g（x）在区间[a，b]上的“绝对和”．
（1）试求函数f（x）=x²与g（x）=x（x+2）（x-4）在闭区间[-2，2]上的“绝对和”．
（2）设h_m（x）=-4x+m及f（x）=x²都是定义在闭区间[1，3]上，记h_m（x）与f（x）的“绝对和”为D_m，如果D（m）的最小值是D（m₀），则称f（x）可用hm0(x)“替代”，试求m₀的值，使f（x）可用hm0(x)“替代”．

下列关于函数f（x）=x²与函数g（x）=2^x的描述，正确的是（　　）

A、?X∈R，当x＞X时，总有f（x）＜g（x）

B、?x∈R，f（x）＜g（x）

C、?x＜0，f（x）≠g（x）

D、方程f（x）=g（x）在（0，+∞）内有且只有一个实数解

定义：两个连续函数（图象不间断）f（x），g（x）在区间[a，b]上都有意义，我们称函数|f（x）+g（x）|在[a，b]上的最大值叫做函数f（x）与g（x）在区间[a，b]上的“绝对和”．
（1）试求函数f（x）=x²与g（x）=x（x+2）（x-4）在闭区间[-2，2]上的“绝对和”．
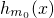（2）设h_m（x）=-4x+m及f（x）=x²都是定义在闭区间[1，3]上，记h_m（x）与f（x）的“绝对和”为D_m，如果D（m）的最小值是D（m₀），则称f（x）可用 $数学公式$ “替代”，试求m₀的值，使f（x）可用 $数学公式$ “替代”．

定义：两个连续函数（图象不间断）f（x），g（x）在区间[a，b]上都有意义，我们称函数|f（x）+g（x）|在[a，b]上的最大值叫做函数f（x）与g（x）在区间[a，b]上的“绝对和”．
（1）试求函数f（x）=x²与g（x）=x（x+2）（x-4）在闭区间[-2，2]上的“绝对和”．
（2）设h_m（x）=-4x+m及f（x）=x²都是定义在闭区间[1，3]上，记h_m（x）与f（x）的“绝对和”为D_m，如果D（m）的最小值是D（m），则称f（x）可用

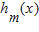“替代”，试求m的值，使f（x）可用

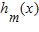“替代”．